[python]双线性插值的原理及实现

kkjz

2021 年 10 月 25 日

533 次浏览

暂无评论

893字数

算法项目

项目地址：

Bilinear_interpolation_with_Python

request:

numpy
opencv

biline.py用数字模拟双线性插值

image.py使用图片测试双线性插值，

双线性插值的问题是解决图像的大小缩放，但是缩放的同时也会有信息的丢失，本质上是一种加权算法。

在了解双线性插值之前，得先说说线性插值。

1.线性插值

请输入图片描述

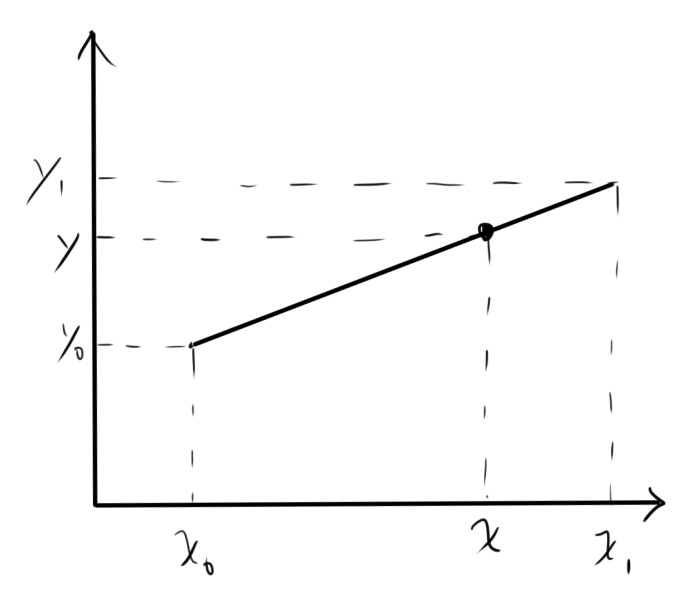
假如我们现在有两个点$ (x_0,y_0)$ 和$ (x_1,y_1)$，$x$点的值已知，现在我们想求中间点$(x,y)$点的y值。由初中的两点确定一条直线可知，我们只要列出：

$$ \frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0} $$

代入$x$即可解出y值，上面公式变换一下即为：

$$ y=\frac{x_1-x}{x_1-x_0}y_0+\frac{x-x_1}{x_1-x_0}y_1 $$

仔细观察变化后的公式可知，y值越靠近哪边的点，哪边的点的y值权重就越大（也就是越像那个点）

若$x$轴代表在某轴上像素点的位置，$y$轴代表该点的像素值，那么我们就可以根据像素点之间的距离得出该位置的像素值。

由于像素之间相隔的距离定为1，所以上面公式中的$ x_1-x_0$定为1，故我们可以设

$$ \alpha=|\frac{x_1-x}{x_1-x_0}| $$

那么另一个权重则为$1-\alpha$，公式可以变成：

$$ y=\alpha y_0+(1-\alpha)y_1 $$

这样做是为了防止$x-x_0<0$的情况导致最后结果为负数。

实现代码：

def single_biline(x,x0,x1,y0p,y1p):
    # w1=(x-x0)/(x1-x0)
    # w2=(x1-x)/(x1-x0)
    # 设 alpha=w1
    # 原理和注释一样，因为像素默认长度为1，所以x1-x0一定为1
    # 使用alpha避免负数的问题
    alpha=abs(x-x0)
    y=alpha*y0p+(1-alpha)*y1p

    return y

2.双线性插值

假设我们现在要将2x2的像素进行双线性插值为1像素：

请输入图片描述

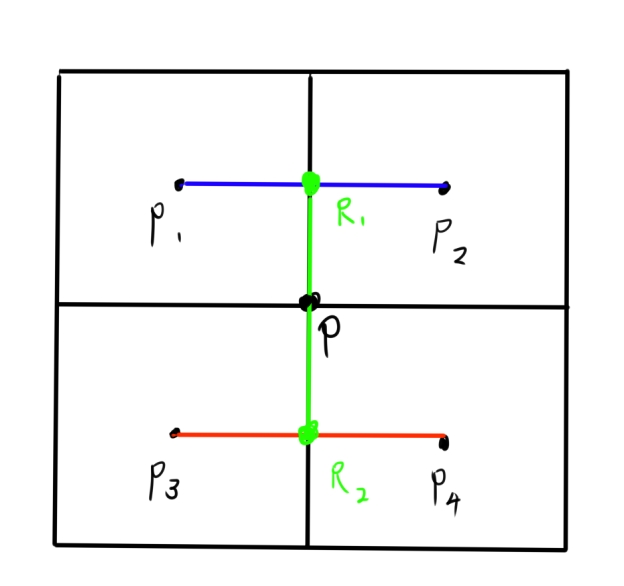
双线性插值，则是线性插值的基础上，再进行三次双线性插值

当然对y轴双线性插值也是一样的结果。

def double_biline(image,ssize,dsize):
    '''
    image: cvform [h,w]
    SSIZE: The size of Source image [h,w]
    DSIZE: The size of Destination image [h,w]
    '''
    result=np.zeros(dsize,dtype=np.uint8)
    ssize=np.array(ssize)
    gece=ge_ce(ssize,dsize)
    # print(gece)
    for i in range(dsize[0]):
        for j in range(dsize[1]):
            # 边界溢出处理
            if gece[i][j][0]<0:
                gece[i][j][0]=0
            if gece[i][j][0]>(ssize[0]-1):
                gece[i][j][0]=ssize[0]-1
     
            if gece[i][j][1]<0:
                gece[i][j][1]=0
            if gece[i][j][1]>(ssize[1]-1):
                gece[i][j][1]=ssize[1]-1
            # print(gece[i][j])

            x0= int(math.floor(gece[i][j][0]))
            x1= int(math.ceil(gece[i][j][0]))
            y0= int(math.floor(gece[i][j][1]))
            y1= int(math.ceil(gece[i][j][1]))

        
            y0p=image[x0][y0]
            y1p=image[x1][y0]
            y2p=image[x0][y1]
            y3p=image[x1][y1]

            p1=single_biline(gece[i][j][0],x0,x1,y0p,y1p)
            p2=single_biline(gece[i][j][0],x0,x1,y2p,y3p)
            p3=single_biline(gece[i][j][1],y0,y1,p1,p2)
            result[i][j]=np.array(p3,dtype=np.uint8)


    return result

3.寻找相对坐标

为了图片的放大和缩小，我们需要寻找原图像素点的位置和目标图像位置点的相对关系。

例如我们原图为4x4的像素，现在要把它变成2x2的像素，设每个像素点的位置在像素点的正中央，则在几何上看来，它们的关系为：

请输入图片描述

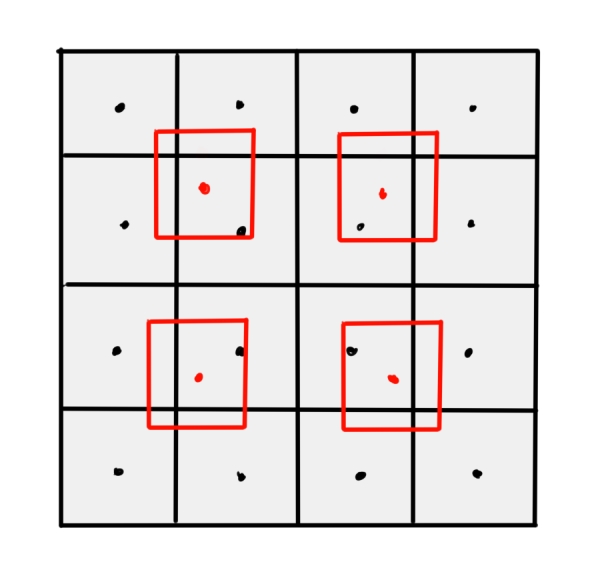
将左上角的点设为原点（0，0），以x轴为例，则目标点对应原图坐标点的位置有如下关系：

$$ x=(x_{des}+1)\frac{L_{src}}{L_{des}+1}-0.5 $$

$x_{des}$为目标图片x坐标

$L_{des}$和$L_{src}$则为目标图片和原图的x轴像素的总个数

y轴同理，则可得出：

请输入图片描述

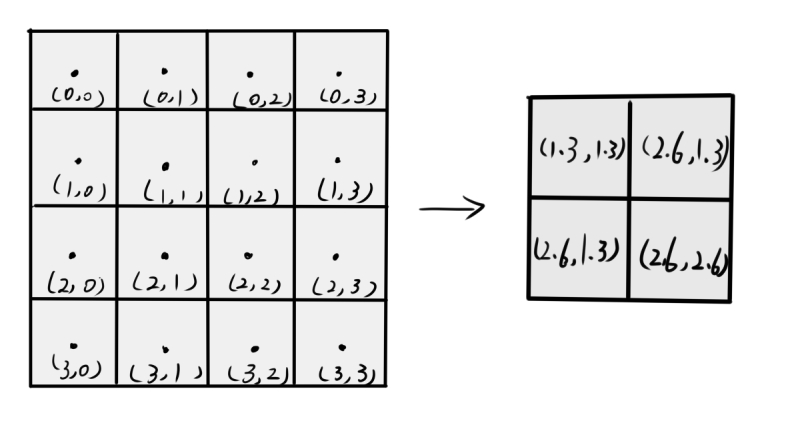
有了像素点之间的位置信息，就可以利用上下界函数ceil和floor函数求得目标点对应原图中的周围四个像素点，再将其带入$y=\alpha y_0+(1-\alpha)y_1$则可求得对应点的像素值。

# 目标图像在原图对应的几何坐标位置,输出对应位置的几何坐标
def ge_ce(ssize,dsize):
    '''
    get the Absolute location in sorce loaction
    '''  
    result=np.zeros([dsize[0],dsize[1],2])
    for i in range(dsize[0]):   
        for j in range(dsize[1]):
            # SrcX=(i+0.5)* (ssize[0]/dsize[0]) -0.5
            # SrcY=(j+0.5)*(ssize[1]/dsize[1])-0.5
            SrcX=(i+1)* (ssize[0]/(dsize[0]+1)) -0.5
            SrcY=(j+1)*(ssize[1]/(dsize[1]+1))-0.5
            result[i][j]=[SrcX,SrcY]

    # 对应（0，0）在图片左上角
    # y,x,c[x,y]
    return result

4.边界处理

以上介绍的是图片缩小的情况，若是将图片放大则有可能出现以下的情况：

请输入图片描述

比如4x4升16x16的情况，会出现第一个点的坐标值(-0.26，-0.26)的情况，这时如果仍使用之前的取上下限，则原图取周围四个点的时候会得到（-1，-1），（-1，0），（-1，0），（0，0）带负数的情况，而原图坐标点是没有负数位置的像素点的。因此我们可以在获得相对坐标的时候，将小于0的数字变成0，0.1。

0的情况就是只取左上角的一个像素，0.1则是取左上角的四个像素的线性插值。

def double_biline(image,ssize,dsize):

    ...
    for i in range(dsize[0]):
        for j in range(dsize[1]):
            # 边界溢出处理
            if gece[i][j][0]<0:
                gece[i][j][0]=0
            if gece[i][j][0]>(ssize[0]-1):
                gece[i][j][0]=ssize[0]-1
   
            if gece[i][j][1]<0:
                gece[i][j][1]=0
            if gece[i][j][1]>(ssize[1]-1):
                gece[i][j][1]=ssize[1]-1
    ....

[python]双线性插值的原理及实现