适用于解决小样本问题,容易被噪音影响
和普通机器学习不同处在于,使用凸优化问题中的二次规划求得最小值而不是梯度下降
求数据数据到分割面距离->间距最大值-> 无约束优化求最小值 -> 求对偶最大值->SMO求解对偶式子->求出w、b的值
解决线性可分问题:
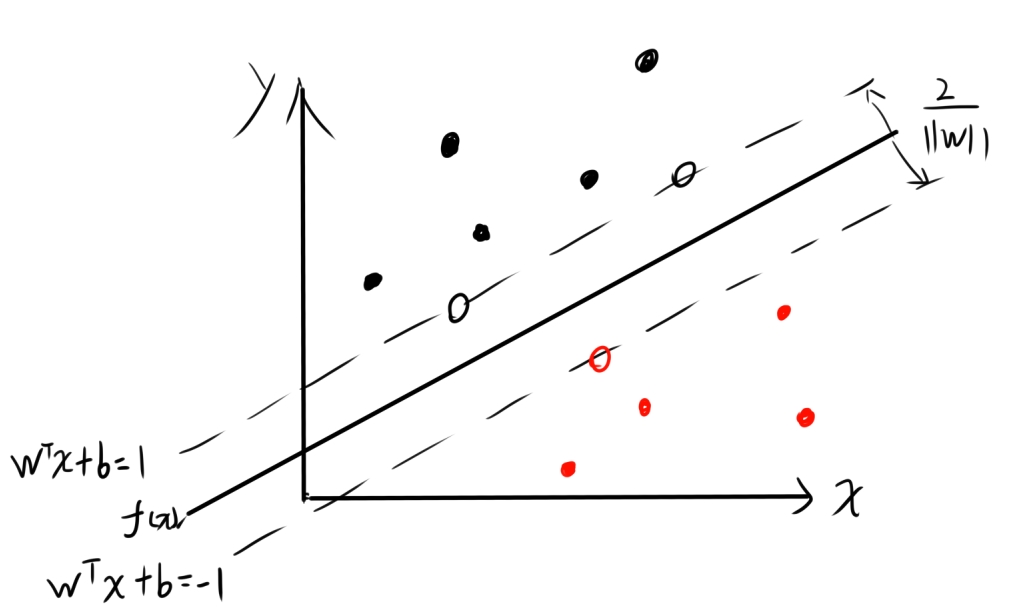
SVM要求寻找一个$ f(x)=w^Tx+b$使得其能够在数据集中找到一条线,能最大化的分割不同种类的数据集
因此要求的两个变量为$ w$和$b$
其中$x=(x_1,x_2,...,x_n)$,$w=(w_1,w_2,...,w_n)$
利用点到超平面的距离公式,可得点到超平面最短距离为:
$$ r=\frac {|w^Tx+b|}{||w||} $$
如SVM能正确分类,则其判断的依据为:
$$ \left\{ \begin{array}{c} w^Tx_i+b\geq+1, y_i=+1 \\ w^Tx_i+b\leq-1, y_i=-1 \end{array} \right. $$
(这里$y_i$是标签值,取别的也可以但是为了方便后面的计算所以取+1和-1)
那么这两个异类超平面上的点(训练集)到$f(x)$的距离之和就为
$$ r=\frac{2}{||w||} $$
因此我们要最大化这个间隔,也就等价于
$$ \begin{gathered} min&\frac{1}{2}||w||^2 \\ s.t.&y_i(w^Tx_i+b)\ge1,&i=1,2,...,m \end{gathered} $$
这就是SVM的基本型
为了求解这个问题,使用对偶问题来求解
对偶问题原理不在这详解了,只讲结果
首先使用拉格朗日乘子法将其转化为$L(w,b,\alpha)$,然后再对其求对偶函数(无约束优化):
$$ L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=0}^m{\alpha_i(1-y_i(w^Tx_i+b))} $$
$$ \theta(\alpha)\le \begin{gathered} max \\ w,b,\alpha \end{gathered} [inf(L(w,b,\alpha))] $$
$\alpha=(\alpha_1,\alpha_2,...,\alpha_n)$
$ inf()$为求取下界的意思。
由SVM的基本型中的限制条件,我们可以推出其$L(w,b,\alpha)$满足KKT条件,即
$$ \left\{ \begin{array}{c} \alpha_i\ge0; \\ y_if(x_i)-1\geq0;\\ \alpha_i(y_if(x_i)-1)=0. \end{array} \right. $$
那么$L(w,b,\alpha)$就满足了强对偶性,即为
$$ \theta(\alpha)=\begin{gathered} max \\ w^*,b,\alpha\end{gathered}[inf(L(w,b,\alpha))] $$
其中$w^*$为$ f(x)=w^Tx+b$的最优解
由于要求$inf(L(w,b,\alpha))$,所以我们要求$L(w,b,\alpha)$的极值点,所以我们对其的$w$和$b$进行微分并置0,
$$ w=\sum^m_{i=1}\alpha_iy_ix_i $$
$$ 0=\sum^m_{i=1}\alpha_iy_i $$
将得到的微分公式带回原式,得到其极值点下的最小值,化简后得:
$$ \begin{gathered} \theta(\alpha)=\begin{gathered} max \\ \alpha\end{gathered}&\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i=1}\sum^m_{j=1}\alpha_i\alpha_jy_iy_jx^T_ix_j \\ s.t& \sum^m_{i=1}\alpha_iy_i=0, \\ & \alpha\ge0,&i=1,2,...,m \end{gathered} $$
可以使用SMO算法将 $ \alpha $解出来(这里需要迭代)
SMO属于二次规划问题
在这里我们不把$w$求出来,而是使用替代:(将上面微分出的$w$的式子带入后化简)
$$ w^Tx=\sum^m_{i=1}\alpha_iy_ix_i^Tx $$
利用KKT的限制条件,把$b$算出来
$$ b=\frac{y_i\sum^N_{j=1}\alpha_jy_jx^Tx}{y_i} $$
最后测试时的公式,对测试样本x就变为
对测试样本X:
若$\sum^N_{i=1}\alpha_iy_iK(x_i,X)+b\ge0 $
则y=1,否则y=0
其中$K(x_i,X)=x^T_iX$
这里可以发现,由于kkt定义的限制,总有$\alpha_i=0 $或者$y_if(x_i)=1 $ ,所以只有当$\alpha_i\ge0$时,这个公式才有意义,换句话说,这个公式只会注意在向量边上的向量点。
这里解释下关系。
在拉格朗日函数$L(w,b,\alpha)$中对于不等式的约束条件中,由于kkt限制条件中的$\alpha_i(y_if(x_i)-1)=0.$所以$\alpha_i=0 $,且$x_i$的点不在向量边上,反过来说若是$1-y_i(w^Tx_i+b)=0$,即$x_i$在向量边上。
通过这个方法,我们可以将非向量边上的$x_i$去掉,减少验证时的计算量。
这样$ f(x)=w^Tx+b$的值就都求出来了
非线性问题:
先映射加维度把问题变成线性可分(也就是用核函数将其映射)将$x^Tx$变为$K(x_1,x_2)$
用核函数就可以解决非线性问题,但是会增加运算的时间