符号解释

⨀ 矩阵连乘（对应位置相乘）

⨂ 卷积

@ 矩阵乘法

特征图大小计算

1.如果计算方式采用'VALID'，则：

$$ w_{out}=\frac{w_{in}-F}{stride}+1 $$

其中$w_{out}$为输出特征图的大小，$w_{in}$为输入特征图的大小，F为卷积核大小，stride为卷积步长。

2.如果计算方式采用'SAME'，输出特征图的大小与输入特征图的大小保持不变，

$$ w_{out}=\frac{w_{in}+2*padding-F}{stride}+1 $$

其中padding为特征图填充的圈数。

若采用'SAME'方式，kernel_size=1时，padding=0；kernel_size=3时，padding=1；kernel_size=5时，padding=3，以此类推

计算感受野（RF）：

上输出，下输入

1。重下往上计算（从输出层开始算）

首先，感受野代表这个像素对应原输入图的映射大小（每个像素对应原图的感受野）

一般默认输出层即为最后一层（你要算感受野的那层）RF=1来开始算，算到要推算的层数，即为该点对应该层的感受野

计算公式为：

$$ RF_n=(RF_n-1)*stride+Ksize $$

计算时，把要计算的层的核尺寸当作本层对上层的感受野RF，然后逐层向上计算，直到算到第一层的RF，即为本层的对应感受野

2.重上往下计算（从输入层开始算）

默认输入的时候，第一层的RF=输入的卷积核大小

$$ S_n=S_{n-1}*s $$

$$ RF_n=RF_{n-1}+(Ksize-1)*S_n-1 $$

• 这里的$s$为该层的stride（输入大小/输出大小）
• $S_n$为到n层为止，所有stride的乘积

PS：FC核size为1

空洞卷积核计算方法

$$ k=k+(k−1)(hloesize−1) $$

常见激活函数

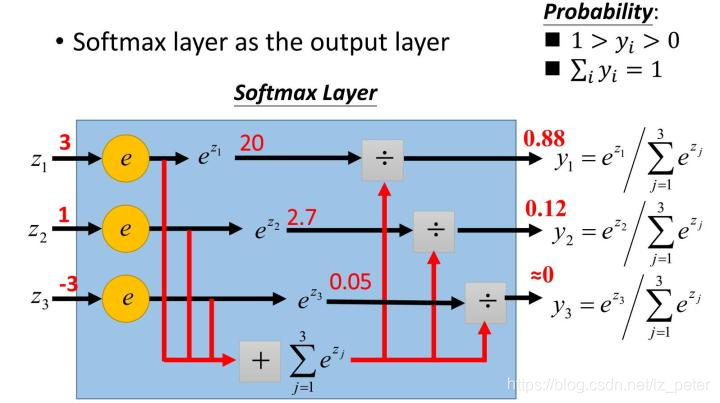
• softmax函数：

  $$ p(y|x_i)=\frac{e^{x_i}}{\sum^C_{c=1}e^{x_c}} $$

  

  

• sigmoid:

  

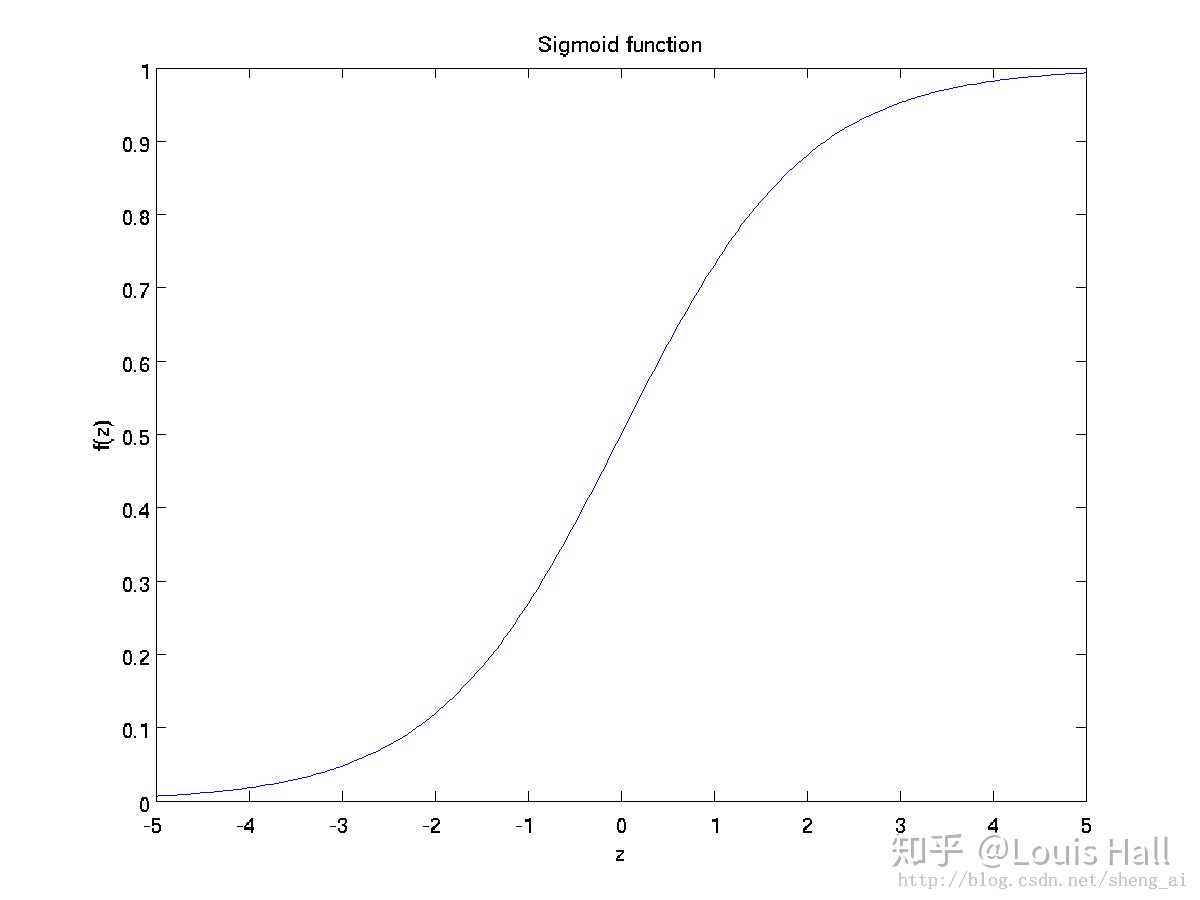
常见loss函数CE交叉熵

1.二分类问题中的CEloss函数（输入数据是softmax或者sigmoid函数的输出）：

• $ x$表示样本，$y$表示真实标签，$a$表示预测输出，$n$表示样本总数量

2.多分类问题中的CEloss函数（输入数据是softmax或者sigmoid函数的输出）：

• 当使用sigmoid作为激活函数的时候，常用交叉熵损失函数而不用均方误差损失函数，因为它可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。