EfficientNet
一种提取特征的分类网络，在ImageNet中取得top-1 accuracy 84.3%的最高成绩，并且比当时的最好的卷积网络要更小和更快
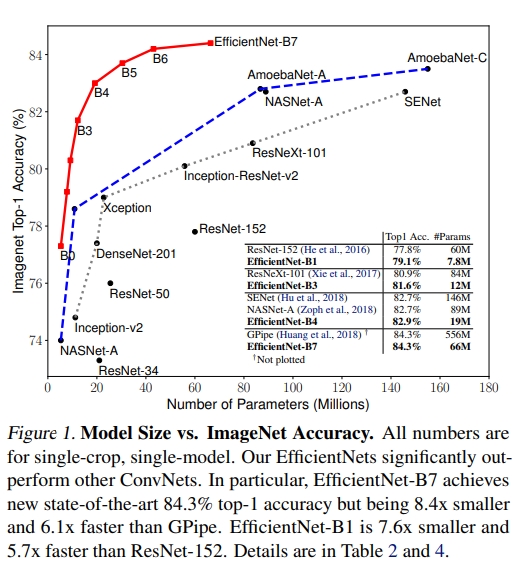
首先，作者总结到目前卷积神经网网络能够通过更深、更宽的网络以及更高的输入分辨率图片，能够使得卷积神经网络获得更好的性能，但是这些增益会随着增加的幅度逐渐减少
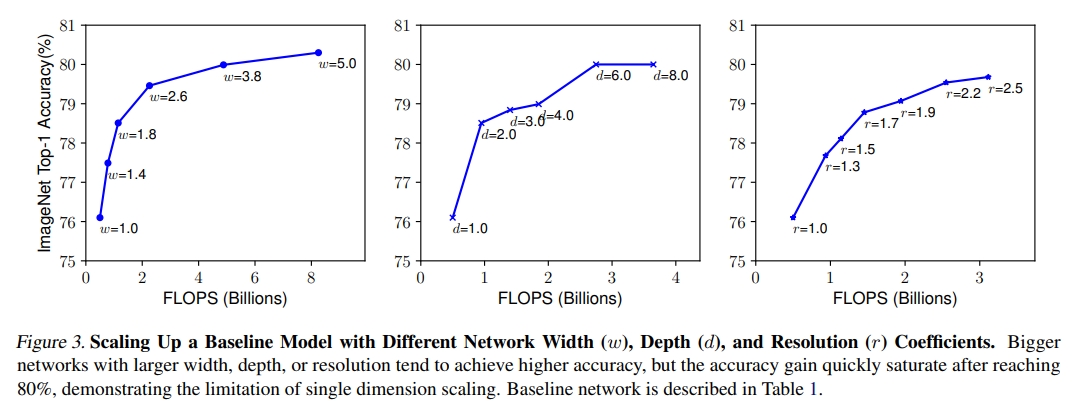作者发现，在Flops数相同的情况下，若是只增加网络的深度d（图中表示为运算量的增加），随着网络参数的增加，网络的性能很快就饱和了；但是在Flops相同的情况下，若是增加网络的宽度w和分辨率r，随着网络参数的增加，网络能够获得更加好的效果
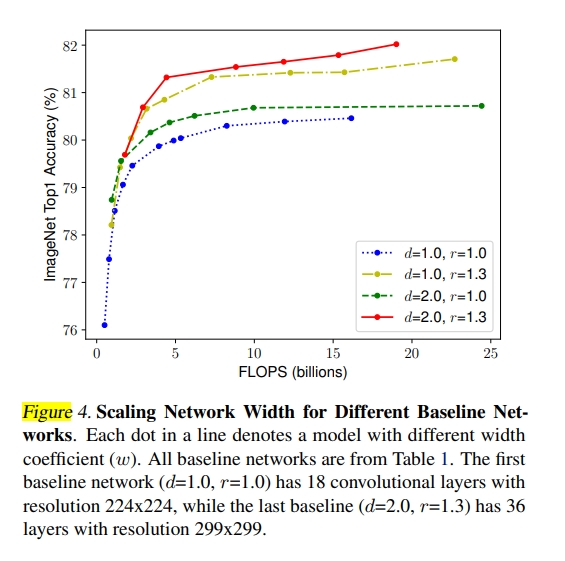
图中的X轴Flops可以看作模型的深度d
因此作者认为，在每种结构的网络中，在增加指定大小Flops的情况下，网络中宽度w，深度d，以及输入的图片分辨率r应该是存在一种比例关系，增加的参数能够使得网络效果增益获得最大化；（换句话说就是如何按比例去分配这些增加的参数使得网络收益最大化）。在文中，作者认为这种比例还存在某种限制条件，可以利用这些限制条件去寻找比例：
$$ depth: d = α^\phi \\ width: w = β^\phi \\ resolution: r = γ^\phi \\ s.t. \ α · β^2· γ^2 ≈ 2 \\\ α ≥ 1, β ≥ 1, γ ≥ 1 $$
$\alpha , \beta , \gamma $分别为卷积层数、卷积层通道数、输入图片分辨率相对于baseline原本数值的倍数
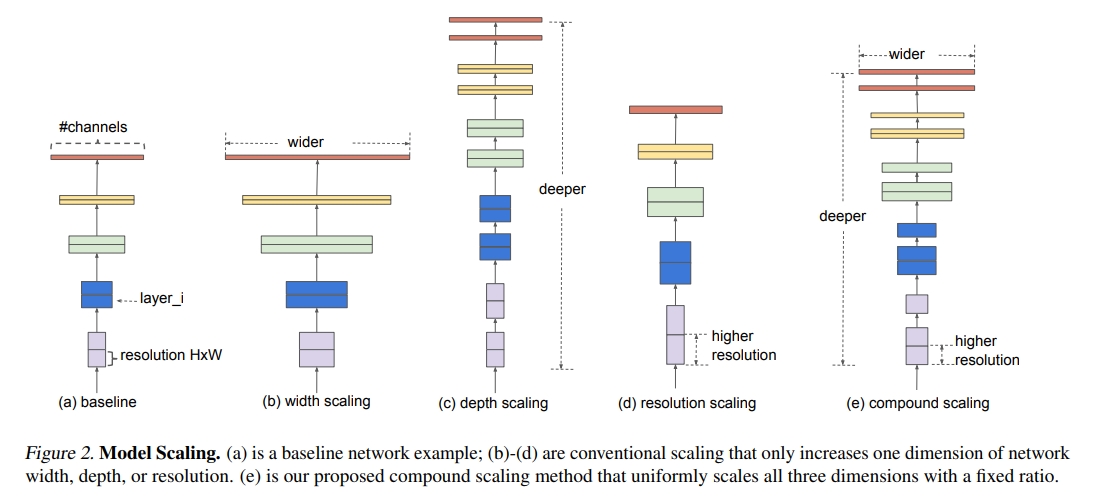
假设某个baseline的Flops为400M，输入尺寸为224x224，卷积层有18层，
以这个baseline为b-0，则有$2^\phi=1$，这个1是baseline的Flops的倍数
则此时$\phi=0$， (d=1.0, r=1.0（$\alpha^0=1,\gamma^0=1$）)
以efficientNet-b0（这个是作者通过NAS找到的）为例子，
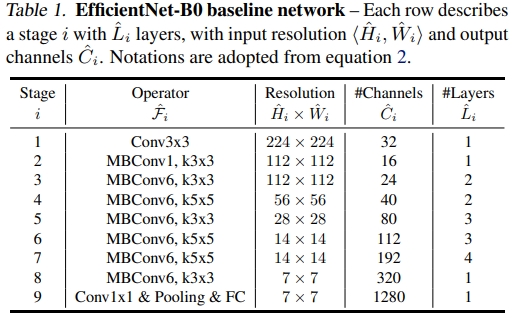
增加Flops的总量后，以$α · β^2· γ^2 ≈ 2 $为限制，网络搜索发现，当$ α = 1.2, β = 1.1, γ = 1.15$时，网络的增益效果最好，于是以上面的公式为例子，推算出来EfficientNet的b1-b7系列：
Coefficients: width,depth,res,dropout
'efficientnet-b0': (1.0, 1.0, 224, 0.2),
'efficientnet-b1': (1.0, 1.1, 240, 0.2),
'efficientnet-b2': (1.1, 1.2, 260, 0.3),
'efficientnet-b3': (1.2, 1.4, 300, 0.3),
'efficientnet-b4': (1.4, 1.8, 380, 0.4),
'efficientnet-b5': (1.6, 2.2, 456, 0.4),
'efficientnet-b6': (1.8, 2.6, 528, 0.5),
'efficientnet-b7': (2.0, 3.1, 600, 0.5),...
reference:efficientnet_builder.py
这些网络比起同量级的分类卷积网络，拥有更小、更快、更准确的优势
题外话：怎么在basebone实现d、w的增加
w的实现：
将所有卷积的通道数直接用 原本大小乘w：
class EfficientNet(nn.Module):
def __init__(self, blocks_args=None, global_params=None):
super().__init__()
...
out_channels = round_filters(32, self._global_params) # number of output channels
self._conv_stem = Conv2d(in_channels, out_channels, kernel_size=3, stride=2, bias=False)
....
-----
def round_filters(filters, global_params):
...
filters *= multiplier
...
d：把block中 原本重复的次数*d
block_args = block_args._replace(
input_filters=round_filters(block_args.input_filters, self._global_params),
output_filters=round_filters(block_args.output_filters, self._global_params),
num_repeat=round_repeats(block_args.num_repeat, self._global_params)
)
...
def round_repeats(repeats, global_params):
"""Round number of filters based on depth multiplier."""
multiplier = global_params.depth_coefficient
if not multiplier:
return repeats
return int(math.ceil(multiplier * repeats))
...SiLU (Swish-1)
待补充....
AutoAugment
待补充....
stochastic depth
待补充....
EfficientDet
将EifficientNet用于目标识别，并提出BiFPN，两者相结合成为EfficientDet，对比起以往的FPN，拥有更好的特征提取性能，并且将BiFPN用于现存的目标检测模型上，都能使其拥有更好的性能、计算消耗更小的特点。
BiFPN
在目标识别中，用于提取小目标的特征，类似EffecientNet的设计思想，作者认为对于不同分辨率的图片应该用不同宽度、深度的FPN网络去解析，所以本质上BiFPN是FPN的一种进阶版本。
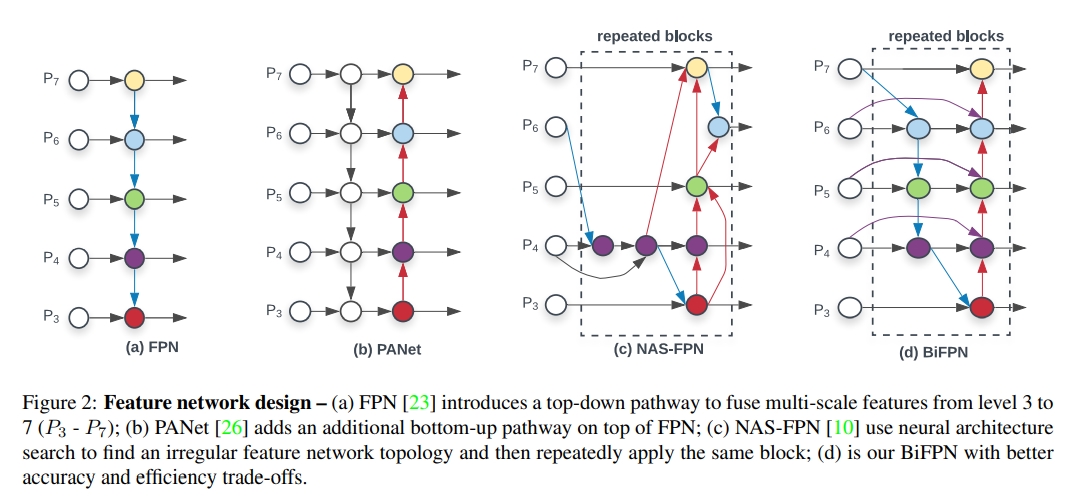开始使用BiFPN一般是当图片已经下采样了$2^3$，也就是经过了3次池化以后（类似FPN）
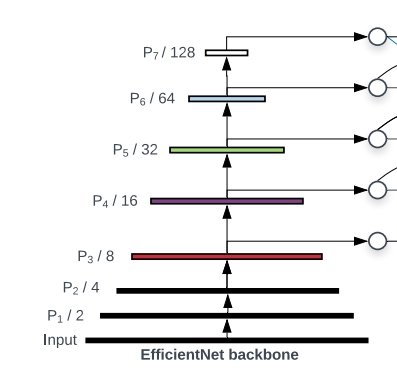
和上面的EfficientNet中一样，$\phi$是主干网络中的参数量的层级
对于BiFPN中的Layer（可以看作一个bin）:
$$ W_{bifpn} = 64*(1.35^\phi), \ D_{bifpn} = 3 + \phi $$
$W_{bifpn}$是卷积核的通道数
$D_{bifpn}$是Layer（也就是bin）的总个数，上图的d就代表一个BiFPN Layer
对于经过BiFPN后的Box/class 预测网络：
$$ W_{pred} = W_{bifpn} \\ D_{box} = D_{class} = 3 + \lfloor \phi/3\rfloor\ $$
$W_{pred}$指的是分类和识别框标记网络中的卷积核通道数，与BifPN中的统一即可
而输出的最大识别框数$D_{box} $和网络可识别的分类数$D_{calss}$则应该根据网络的参数大小变化而变化
对于*输入的图片分辨率rR：
$$ R_{input}=512+\phi *128 $$
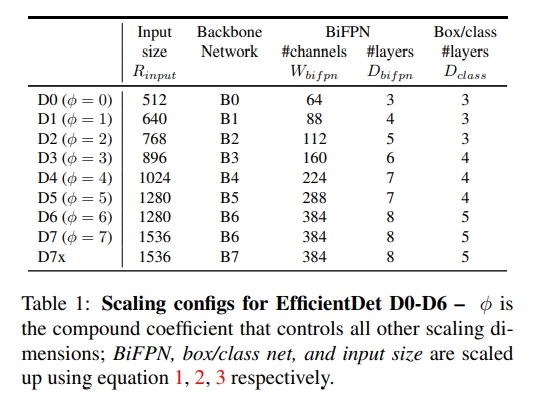
以EfficientNet-b0的框架作为backbone，生成EffcientDet-D0，其结构由FPN改变的faster-rcnn转变而来：
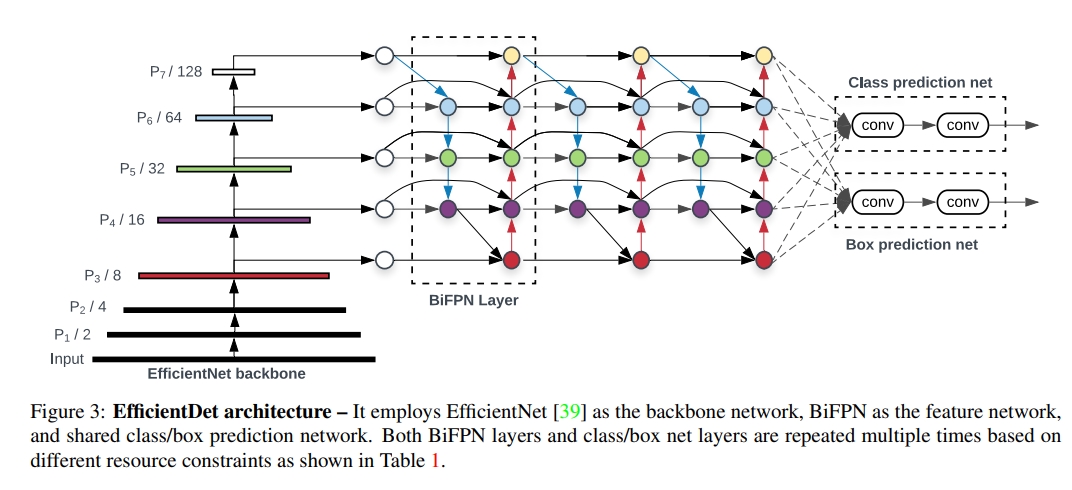
D0的$\phi=0$,结合上面的公式可推出至D7的框架：
Weighted Feature Fusion:
在每个BiFPN layer中，需要融合不同分辨率的特征的时候，作者认为不同分辨率对于不同大小的目标对输出的贡献是不一样的，于是作者决定使用权重来配合尺度融合
这里最终决定了使用Fast normalized fusion:（它类似softmax，效果比单用softmax差，但是速度更快
$$ O=\sum_i \frac{w_i}{\epsilon+\sum_jw_j}*I_i $$
$w_i$是输入上的权重、$I_i$是输入、$\sum_jw_j$指所有输入的权重
$w$是经过Relu处理的，所以都存在$w\ge0$，$\epsilon=0.0001$，防止分母为0
Fast normalized fusion起到了类似激活函数的作用，将输出映射到0-1
详解BiFPN内部结构：
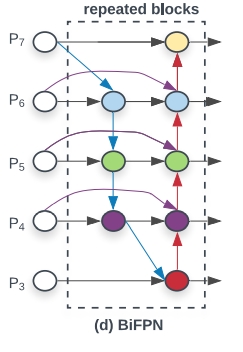
拿$P_6$来说，有
$$ P^{td}_6=Conv(\frac{w_1*P^{in}_6+w_2*Resize(P^{in}_7)}{w_1+w_2+\epsilon}) \\ P^{out}_6=Conv(\frac{w_1'*P^{in}_6+w_2'*P^{td}_6+w_3'*Resize(P^{out}_5)}{w_1'+w_2'+w_3'+ \epsilon}) $$
$P^{td}_6$指中间量，$P^{out}_6$是输出量
$w$则是上面指的不同尺寸融合时的权重系数
$Resinze()$用的是双线性插值
$Conv()$文中使用的是 depthwise separable convolution（mobileNet中的可分离卷积）
$\epsilon$是超参，防止分母为0