离散概率分布
二项分布
1)做某件事次数是固定的,用n表示
2)每一次事件都有两个可能的结果(成功,或者失败)
3)每一次成功的概率都是相等的,成功的概率用p表示
4)你感兴趣的是成功x次的概率是多少
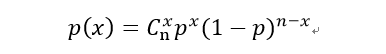
其中二项分布的$E(x)=np=u$
抛硬币5次(n),恰巧有3次正面朝上(x=3,抛硬币正面朝上概率p=1/2),可以用上面的公式计算出出概率为31.25%
伯努利分布
$$ f(x)=p^x(1-p)^{1-x} $$
其中x=0或1 即为成果或者不成功
假设你要生孩子,生男孩子概率p,生女孩纸概率1-p
伯努利实验:生一次孩子
伯努利分布:生一次孩子,生男孩子概率为p,生女孩纸概率1-p,这个就是伯努利分布
n重伯努利实验:将伯努利实验重复n次,就是生n次孩子。
二项分布:n重伯努利试验「成功」次数的离散概率分布,拿投硬币来说,投5次硬币的二项分布即为:
举个例子,二项分布的x=1时,若用伯努利分布来实现的话就是:
$$ C^1_5*f(1)^1*f(0)^4=5*[p^1*(1-p)^{1-1}]^1*[p^0*(1-p)^{1-0}]^4 $$
就是做伯努利1次成功、4次失败的概率,5是指可能投的第一次出现、或者第二次出现....第五次出现
几何分布
1)做某事件次数(也叫试验次数)是固定的,用n表示
(例如抛硬币3次,表白5次),
2)每一次事件都有两个可能的结果(成功,或者失败)
(例如每一次抛硬币有2个结果:正面表示成功,反面表示失败。
每一次表白有2个结果:表白成功,表白失败)。
3)每一次“成功”的概率都是相等的,成功的概率用p表示
(例如每一次抛硬币正面朝上的概率都是1/2。
假设你是初出茅庐的小伙子,还不是老油条,所以你表白每一次成功的概率是一样的)
4)你感兴趣的是,进行x次尝试这个事情,取得第1次成功的概率是多大。
(例如你在玩抛硬币的游戏,想知道抛5次硬币,只有第5次(就是滴1次成功)正面朝上的概率是多大。
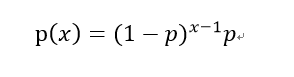
其中 E(x)=1/p,代表一次成功的平均次数
泊松分布
1)事件是独立事件
(类似抽奖这样的就是独立事件)
2)在任意相同的时间范围内,事件发的概率相同
(例如1天内中奖概率,与第2天内中间概率相同)
3)你想知道某个时间范围内,发生某件事情x次的概率是多大
(例如你搞了个促销抽奖活动,想知道一天内10人中奖的概率)
对比二项分布,泊松分布不需要知道p的值,只需要知道这段时间内发生的平均次数u,例如下面的例子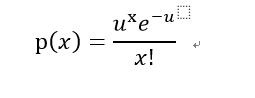
例如你搞了个促销抽奖活动,只知道1天内中奖的平均个数为5个,你想知道1天内恰巧中奖次数为7的概率是多少?
此时x=7,u=5(区间内发生的平均次数),代入公式求出概率为10.44%。Excel中的函数为POISSON.DIST就可以立马算出来。
其中泊松分布的期望和方差都是u
泊松分布的现实意义是什么,为什么现实生活多数服从于泊松分布? - 知乎 (zhihu.com)
连续概率分布
抽样分布有三大应用:T分布、卡方分布和Γ分布
以简单用四个字概括它们的作用:“以小博大”,即通过小数量的样本容量去预估总体容量的分布情况。
即当我们需要用一些小样本寻找整体分布的时候,可以用的方法
1.正态分布
也叫做高斯分布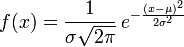
数学期望为$μ$、方差为$σ^2$
因此,求一组数据的期望$μ$、方差$σ^2$就可以求得该样本的总体分布
2.卡方分布
若n个相互独立的随机变量$ξ_1,ξ_2,⋯,ξ_n$,均服从标准正态分布,则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量$X()$,其分布规律称为卡方分布。记作:
$$ \chi \sim \chi^2(k) $$
其密度函数为:
$$ f_k(x)=\frac{(1/2)^{k/2}}{\Gamma(k/2)}x^{\frac k 2 -1}e^{-\frac x 2} $$
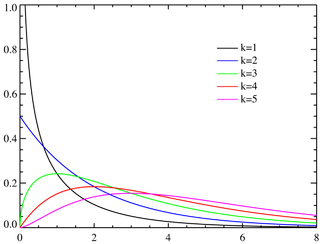
其中k为自由度
关于自由度:设$X_1,X_2,...,X_n$为来自总体N(0,1)的样本,则称统计量
$$ \chi^2=X_1+X_2+...+X_n $$
服从自由度为n的卡方分布,计为$ \chi \sim \chi^2(k)$
一个式子中独立变量的个数称为这个式子的“自由度”
若式子包含有n个独立的随机变量,和由它们所构成的k个样本统计量,则这个表达式的自由度为$n-k$.
比如中包含$ξ_1,ξ_2,...,ξ_n$这n个独立的随机变量,同时还有它们的平均数$ξ$这一统计量,因此,其中任意一个变量为:
$$ ξ_i =ξ -(ξ_1+ξ_2+...+ξ_{i-1}+ξ_{i+1}+...+ξ_n) $$
显然$(1≤i≤n)$,因此自由度为$n-1$.
简单说,n 个样本,如果在某种条件下,样本均值是先定的 (fixed),那么只剩 n-1个样本的值是可以变化的。
$\Gamma$代表Gamma函数,一般对应的$\Gamma(k/2)$的值都有对应的表可以查询
自由度为 k 的卡方变量的平均值是 k,方差是 2k。
卡方分布的应用:
https://cloud.tencent.com/developer/article/1010577
2.1独立性检验:
研究变量之间的关联性,比如男女性别 对 是否赞同在公测吸烟 有显著影响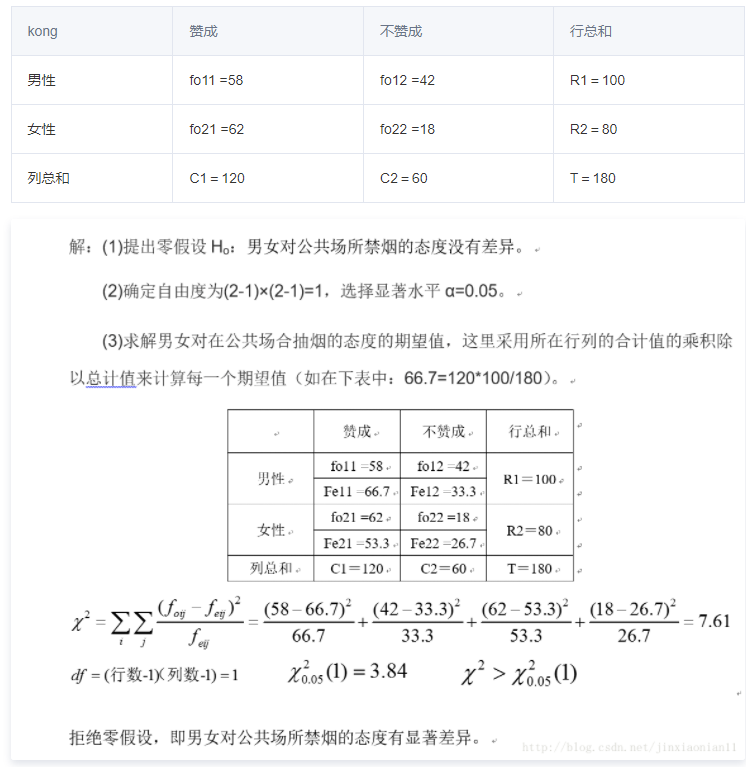
2.2拟合性检验:
单个多项分类名义型变量各分类间的实际观测次数与理论次数之间是否一致的问题, 如赞成和反对的人是否有显著差异
偏差
在机器学习中,度量学习算法的预测结果和真实结果的偏差,即算法本身的拟合能力
在回归算法中,使用学习算法的 所有 平均期望 - 真实值的差的平方,就是这个算法的偏差值bias
$$ bias^2(x)=(\bar f(x)-y)^2 $$
方差
在机器学习中,使用同样数目的不同样本,的差的平方为该学习算法的方差var,代表数据对算法的扰动程度
$$ var(x)=E_D[(f(x;D)-\bar f(x))^2] $$
- 方差:方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
- 协方差: 标准差与方差是描述一维数据的,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
协方差矩阵:
首先说一下多变量向量:当变量多了,超过两个变量了。那么,就用协方差矩阵来衡量这么多变量之间的相关性。假设 X 是以 n个随机变数(其中的每个随机变数是也是一个向量,当然是一个行向量)组成的列向量:
$$ X= \left[ \begin{array}{cc|r} X_1 \\ X_2 \\ ...\\ X_n \end{array} \right] $$
使用多变量向量组成的协方差,称为协方差矩阵: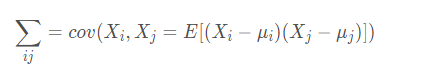
其中$\mu_i$和$\mu_j$代表第i和第j个样本的均值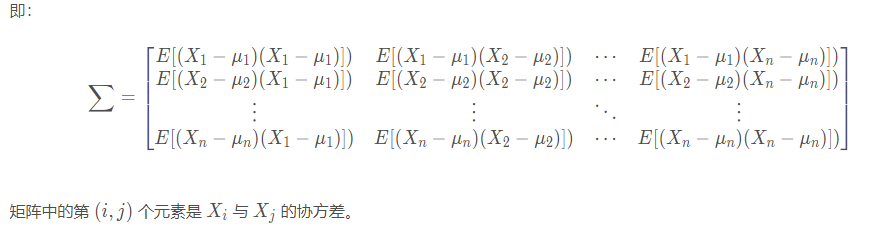
熵
0.自信息
评价、量化某一个概率的不确定的程度
$$ I(x)=-logp(x) $$
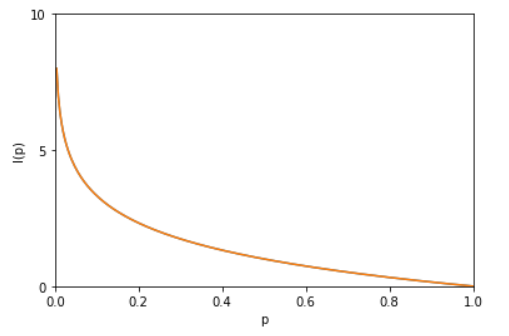
概率越低,自信息越高
ps:
$$ I(x,y)=I(x)+I(y) \\ p(x,y)=p(x)p(y) $$
1.信息熵
评价某一个概率分布的不确定的量(个数),一般说某个随机变量的熵就是指信息熵
$$ H(X)=-\sum_x p(x)log \ p(x)=-E_{x \sim P}[log \ p(x)] $$
其中$X=[x_1,x_2,......x_n]$
若随机变量的个数越多,那么状态也就越多,信息熵也就越大,$H(X)$是对所有可能发生的事件产生的信息量的期望。且$x$取值的个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大
$$ 0 \le H(X) \le log(n) $$
$n$是$x$取值的个数
example:
情况1:x=[0,1,2,3,4,5], p=[0, 0.1, 0.2, 0.3, 0.4]
情况2:y=[0,1,2,3,4,5],p=[0.1, 0.2, 0.2, 0.2, 0.3]
情况1的H(x)>情况2的H(y),均匀分布比非均匀分布的熵要大在多维情况下,可推出联合熵:
$$ H(X,Y)=-\sum_{x,y} p(x,y)log \ p(x,y)=-\sum^n_{i=1} \sum^m_{j=1} p(x_i,y_j)log \ p(x_i,y_j)\\=-E_{x,y \sim P}[log \ p(x,y)] $$
2.条件熵
评估已知x的情况下,y分布的不确定性
$$ H(Y|X)=\sum_xp(x)H(Y|X=x)=-\sum_x p(x) \sum_y p(y|x)log \ p(y|x) $$
有:$H(Y|X)=H(X,Y)-H(x)$
3.相对熵(KL散度)
评价两个概率分布的总体相似程度
$$ D_{KL}(p||q)=\sum_xp(x)log \frac{p(x)}{q(x)}=E_{p(x)}log\frac{p(x)}{q(x)} $$
性质:
1.不对称性:$D_{KL}(p||q) \neq D_{KL}(q||p) $
2.$ D_{KL}(p||q) \ge 0$
4.交叉熵
设$p(x)$为真实分布,$q(x)$为机器的模拟真实的分布
$$ H(p,q)=\sum_xp(x)log\frac{1}{q(x)}=-\sum_x p(x)log \ q(x) $$
其中有:
$$ D_{KL}(p||q)=H(p,q)-H(p) $$
pytorch的loss 交叉熵loss就是用KL散度+信息熵实现的
在机器学习中,由于训练集中的分布是不会变的,所以$H(p)$的值就不会变,可以当作常数,因此
计算最小化$D_{KL}$等价于计算最小化交叉熵,也等价于最大化似然函数$q(x)$
reference:
概率分布
0.概率分布 和 概率密度
在连续的概率分布中:
概率分布函数为:F(x)
概率密度函数为:f(x)
二者的关系为:$f(x) = \frac{dF(x)}{dx}$
即:密度函数f 为分布函数 F 的一阶导数。或者分布函数为密度函数的积分。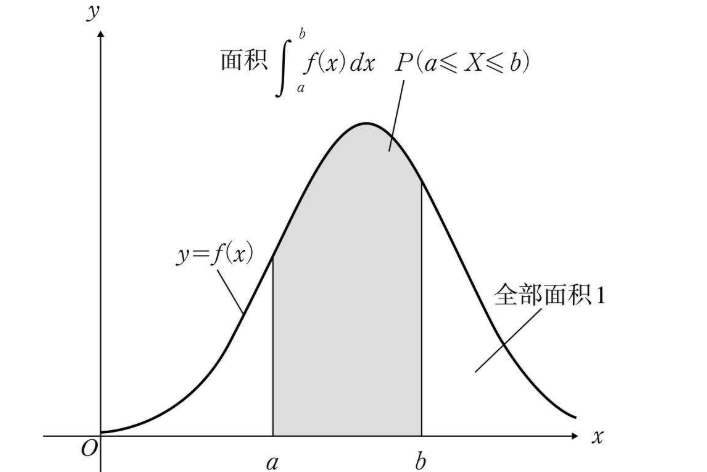
离散的关系则为:$F(X)=\sum_X f(X=x)$
1.边缘概率:
求一个子集的概率分布,这种分布叫做边缘概率分布
离散变量:
$$ P(X)=\sum_y P(X=x,Y=y) $$
连续变量:
$$ p(x)=\int p(x,y)dy $$
2.条件概率的链式法则
$$ P(X^{(1)},...,X^{(n)})=P(X^{(1)})\prod^n_{i=2}P(X^{(i)}|X^{(i)},...,X^{(i-1)})\\ P(a,b,c)=P(a|b,c)P(b,c)\\ P(b,c)=P(b|c)P(c)\\ P(a,b,c)=P(a|b,c)P(b|c)P(c) $$
频率派 最大似然估计
不断比较 真实值与model值的 似然函数最大值 而推算出的$\theta$值 求得一个近似解
似然函数
一句话:模拟真实分布的函数
假设有一个m个样本的数据集$\chi$,它以真实数据生成生成,现在利用$\theta$生成一个模拟真实概率分布$p_{data}(x)$的函数,我们称之为$p_{model}(x;\theta)$,它被用来模拟估计真实的概率分布$p_{data}(x)$,
$p_{model}(x;\theta)$就称为似然函数
$p_{data}(x)$可以理解成一个输出的概率分布,比如输入x=0输出y=1,输入x=1,输出y=0
最大似然估计 MLE
目的是为了评价两个分布之间的相似程度,对于相似的概率分布,我们相信
对于相同的数据,两个分布存在这样的相似条件:
($ \theta $为一组参数,例如各个w的取值范围
这里使得$\ p_{model}(\chi;\theta)$最大时$ \theta $的取值)
$$ \theta_{ML}=\operatorname{arg\,max}_\theta \ p_{model}(\chi;\theta)=\operatorname \ \underset{\theta}{arg\,max} \prod^m_{i=1} p_{model}(x^{(i)};\theta) \\ \approx \theta_{Data} $$
这里的$\theta_{Data}$指我们认为真实的数据中存在$\theta_{Data}$使得数据$\chi$能够产生真实的分布$p_{data}(x)$,
$$ \theta=\operatorname \ \underset\theta{arg\,max} \ p_{data}(\chi;\theta) \ =\operatorname \ \underset\theta{arg\,max} \ \prod^m_{i=1} p_{data}(x^{(i)};\theta) $$
为了防止计算的时候数据下溢和方便计算
可加上对数变为对数似然函数,并且进行缩放时arg max也不会改变,因此再加上求均值,故有:
$$ \theta_{ML}=\operatorname{arg\,max}_\theta \ E_{x\sim \hat{p}_{data}}log \ p_{model}(x;\theta) \approx E_{x\sim \hat{p}_{data}}log\ \hat{p}_{data}(x) $$
其中$E_{x\sim \hat{p}_{data}}$表示在真实数据中取得的x值拿来做平均
因此,为了评估真实分布与预测的分布的差异程度,我们就可以利用KL散度(相对熵)做预测:
$$ D_{KL}(\hat{p}_{data}||p_{model})=E_{x\sim \hat{p}_{data}}[log\ \hat{p}_{data}(x)-log \ p_{model}(x;\theta)] $$
训练模型时,若是使用KL散度作为loss,只要最小化右边的
$$ -E_{x\sim \hat{p}_{data}}log \ p_{model}(x;\theta) $$
就可以了,这也是交叉熵的由来
缺点就是数据比较少的时候容易overfit
线性回归作为最大似然(均方差 可用来 最大化条件对数似然 的证明):
需要条件对数似然结合高斯分布:
若样本是独立同分布的,最大化条件对数似然为:
$$ \theta_{ML} =\operatorname{arg\,max}_\theta \ p_{model}(Y|\chi;\theta) \ =\operatorname{arg\,max}_\theta \ \prod^m_{i=1} p_{model}(y^{(i)}|x^{(i)};\theta)\\ =\operatorname{arg\,max}_\theta \ \sum^m_{i=1} log \ p_{model}(y^{(i)}|x^{(i)};\theta) $$
我们定义$p_{model}(y|x)$的概率分布满足高斯分布,即:
$$ p_{model}(y|x)=N(y;\hat y(x;w),\sigma^2) $$
$\hat y(x;w)$代表在$w$下,高斯分布$p_{model}(y|x)$的均值,因为高斯分布的概率密度函数为:
$$ p(x^{(i)};\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x^{(i)}-\mu)^2}{\sigma^2}) $$
由于这里训练集是离散的,于是可将其带入可得:
$$ \sum^m_{i=1} log \ p_{model}(y^{(i)}|x^{(i)};\theta) \\ =-m \ log\sigma-\frac{m}{2}log(2\pi)-\sum^m_{i=1}\frac{||\hat y^{(i)}-y^{(i)}||^2}{2\sigma^2} $$
对比均方差:
$$ MSN_{train}=\frac{1}{m}\sum^m_{i=1}||\hat y^{(i)}-y^{(i)}||^2 $$
可知,我们要最大化关于$w$条件对数似然只要求最小化的关于$w$的均方差即可
最大后验估计(MAP)
也是点估计,结合了贝叶斯统计的先验概率和最大似然的优点:
$$ \theta_{MAP}=argmax_{\theta} \ p(\theta|x)=argmax_{\theta} \ log \ p(x|\theta)+logp(\theta) $$
如果先验$p(\theta)$的分布是$N(w;0,\frac{1}{\lambda}I^2)$,那么正则化项就正比于$\lambda w^Tw$
比起最大似然,由于先验概率能减少方差,但是增加了偏差
贝叶斯统计派
贝叶斯统计
$D$为训练集
$\theta$为模型参数
$x^*$为要预测的新数据
与最大似然求得一个$\theta$点的值不同,贝叶斯统计是利用训练集算出$\theta$的概率分布,然后利用这个分布$p(\theta|D)$得出预测值$p(\hat y|x^*,D)$或者是下一个$x^*$值的概率分布,优点是可以利用先验知识$p(\theta)$,缺点是容易高偏差。
求预测值:
$$ p(\hat y|x^*,D)=\int_\theta p(\hat y |x^*,\theta)p(\theta|D)d\theta $$
求$x^*$的概率分布:
$$ p(x^*|D)=\int_\theta p(x^*|\theta)p(\theta|D)d\theta $$
贝叶斯线性回归
使用贝叶斯线性方法进行线性回归
给定训练样本$(X,y)$,可以表示成
$$ y=Xw $$
可得出我们的目标是求$p(w|X,y)$,也就是$\theta$的概率分布,利用贝叶斯定理,可以得到:
$$ p(w|X,y)\varpropto p(y|X,w)p(w) $$
由于最终我们使用$p(\theta|D)$的时候是要积分的,因此计算的时就可以舍去所有不含$w$的项,也就是上式使用等价符号的原因
将y表示为方差为1的高斯条件分布可以得到:
$$ p(y|X,w)=N(y;Xw,I)\\ \varpropto exp(-\frac{1}{2}(y-Xw)^T(y-Xw)) $$
$I$为方差为1,协方差为0的协方差矩阵
我们一般会假设一个均匀、熵很大的分布来确定先验概率,这样能表达它的高度不确定性:实数值参数常使用高斯作为先验分布:
$$ p(w)=N(w;\mu_0,\Lambda_0)\varpropto exp(-\frac{1}{2}(w-\mu_0)^T \Lambda_0^-1 (w-\mu_0)) $$
其中$\mu_0$是由$w$(也就是$\theta$)得出的均值
$\Lambda_0$是$w$得出的协方差矩阵
当$\Lambda_0=\frac{1}{\alpha}I$时,贝叶斯线性回归器的正则化项就为$\alpha w^Tw$
不能将先验概率p(w)初始化为无限长
有了条件概率$p(y|X,w)$和先验概率$p(w)$,就可以计算后验概率$p(w|X,y)$了:
$$ p(w|X,y)\varpropto p(y|X,w)p(w) \\ \varpropto exp(-\frac{1}{2}(w-\mu_m)^T \Lambda_m^-1 (w-\mu_m))\\ \varpropto N(w;\mu_m,\Lambda_m) $$
其中$\Lambda_m=(X^TX+\Lambda_0)^{-1}$和$\mu_m=\Lambda_m(X^Ty+\Lambda^{-1}_0\mu_0)$
这样,我们就得到一个符合高斯分布的等价$p(\theta|D)$的等价式了
其中$\mu_m$等于后验概率$p(w|X,y)$的极值
我们可以利用$N(w;\mu_m,\Lambda_m)$求得$w$的取值范围
总结一下:
reference: