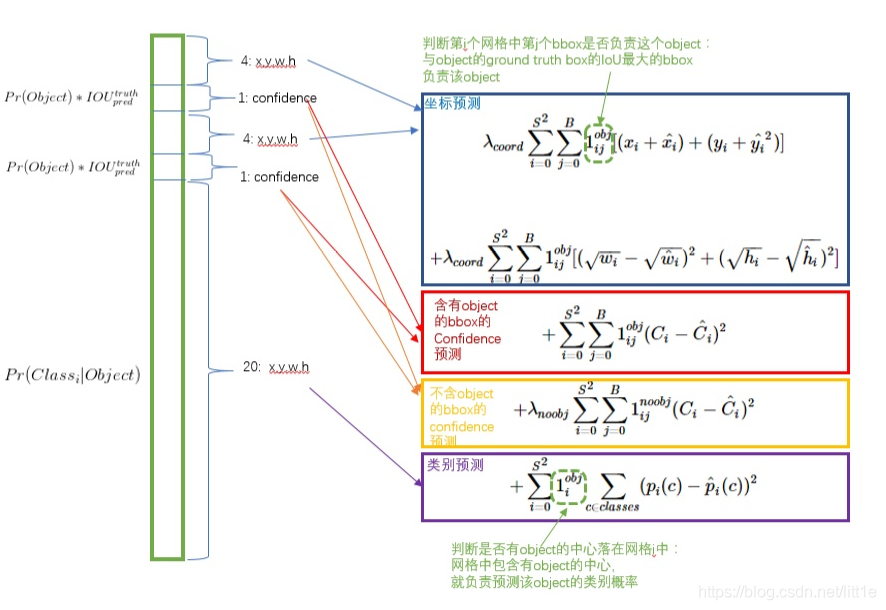
YoloV1
x,y,w,h中的值都是0~1,代表了所指框中,物体所在的框中的位置比例
anchor box:
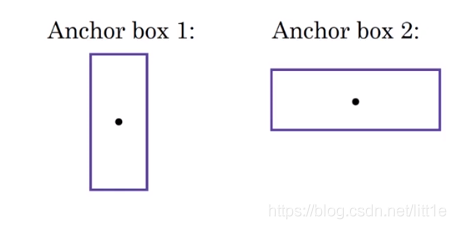
两个anchor box代表不同大小的选择大小
网络结构借鉴了 GoogLeNet 。24个卷积层,2个全链接层,主干网络用的是GooleNet
直接在输出层回归bounding box的位置和bounding box所属的类别(整张图作为网络的输入,把 Object Detection 的问题转化成一个 Regression 问题

缺陷:
YOLO对相互靠的很近的物体(挨在一起且中点都落在同一个格子上的情况),还有很小的群体 检测效果不好,这是因为一个网格中只预测了两个框,并且只属于一类。
测试图像中,当同一类物体出现的不常见的长宽比和其他情况时泛化能力偏弱。
由于损失函数的问题,定位误差是影响检测效果的主要原因,尤其是大小物体的处理上,还有待加强。
YoloV2(YOLO9000)
1.YOLOv2网络通过在每一个卷积层后添加batch normalization,BN 的做法是 在卷积池化之后,激活函数之前,对每个数据输出进行规范化(均值为 0,方差为 1)
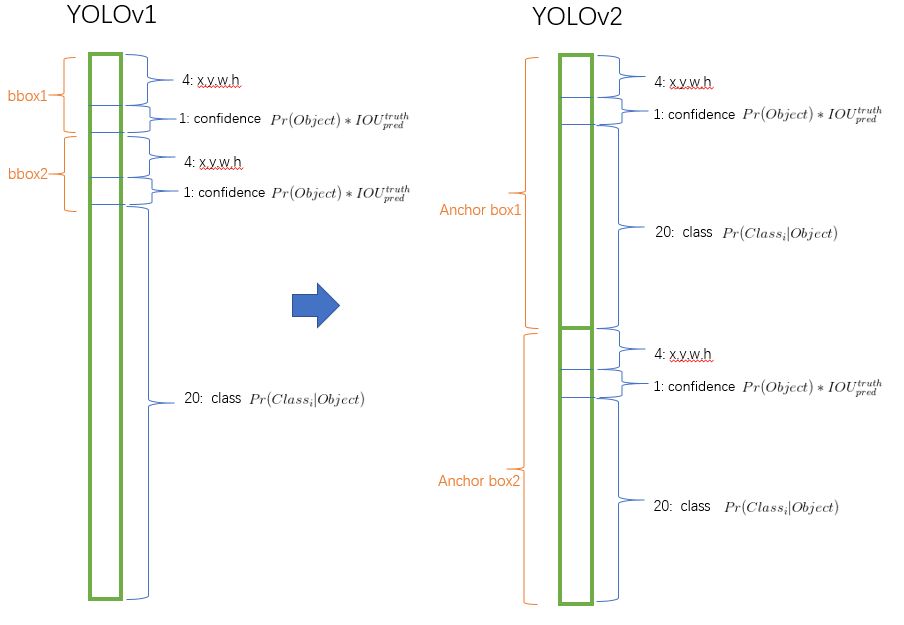
2.YOLOv2移除了YOLOv1中的全连接层(这是DarkNet快的关键)而采用了卷积和anchor boxes来预测边界框。
3.YOLOv2不是采418×418图片作为输入,而是采用416×416大小
4.YOLOv2中引入anchor boxes,输出feature map大小为13×13,每个cell有5个anchor box预测得到5个bounding box,一共有13×13×5=845个box。增加box数量是为了提高目标的定位准确率
5.利用多尺度输入提高了模型的检测能力

V2中的anchor boxes改进:
待补充ing可以先看看下面这个
https://zhuanlan.zhihu.com/p/25167153
dimension clusters?:
作者并没有手动设定 anchor,而是在训练集的 b-box 上用了 k-means 聚类来自动找到 anchor。
类似于k-mean的分类,目的是利用众多的识别结果确认一个正确的目标位置

作者最终选取5个聚类中心作为先验框
Q:YOLO2岂不是一次最多只能判断5个目标?
不是 只是anchor用5种而已,回想一下怎么在训练集上确定anchor的w和h
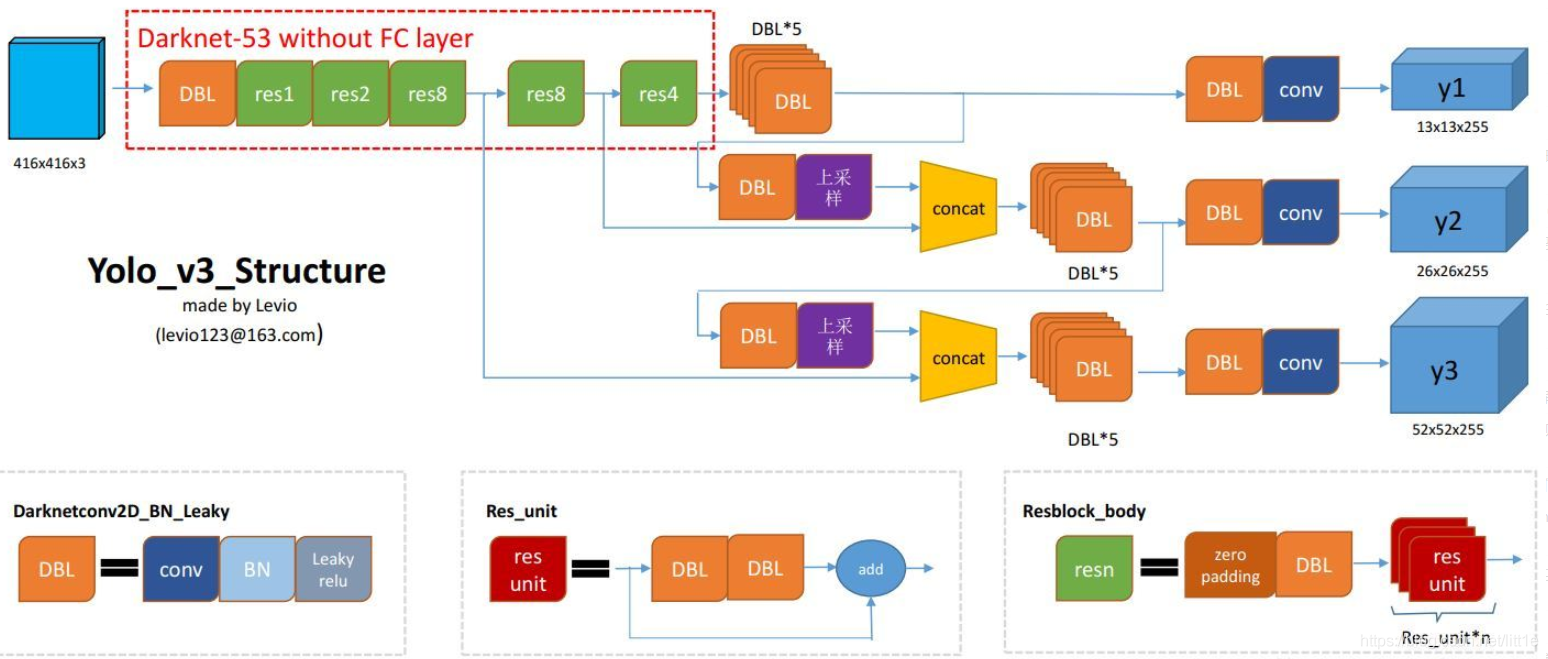
YOLOV3
(https://blog.csdn.net/litt1e/article/details/88907542)
- 摒弃了POOLing,用conv的stride来实现降采样
- 利用类似FPN的方法加强对小目标的检测精度
- 三次检测,分别是在32倍降采样,16倍降采样,8倍降采样时进行检测
不同于faster R-CNN的是,yolo_v3只会对1个prior进行操作,也就是那个最佳prior。
FRCNN中会对每个输出前景判定为1的anchor进行预测
而YOLOV3中的logistic回归就是用来从9个anchor priors中找到objectness score(目标存在可能性得分)最高的那一个。logistic回归就是用曲线对prior相对于 objectness score映射关系的线性建模。
- Bounding box它输出的是框的位置(中心坐标与宽高),confidence以及N个类别。
anchor box只是一个尺度即只有宽高。
ref:
https://blog.csdn.net/litt1e/article/details/88907542
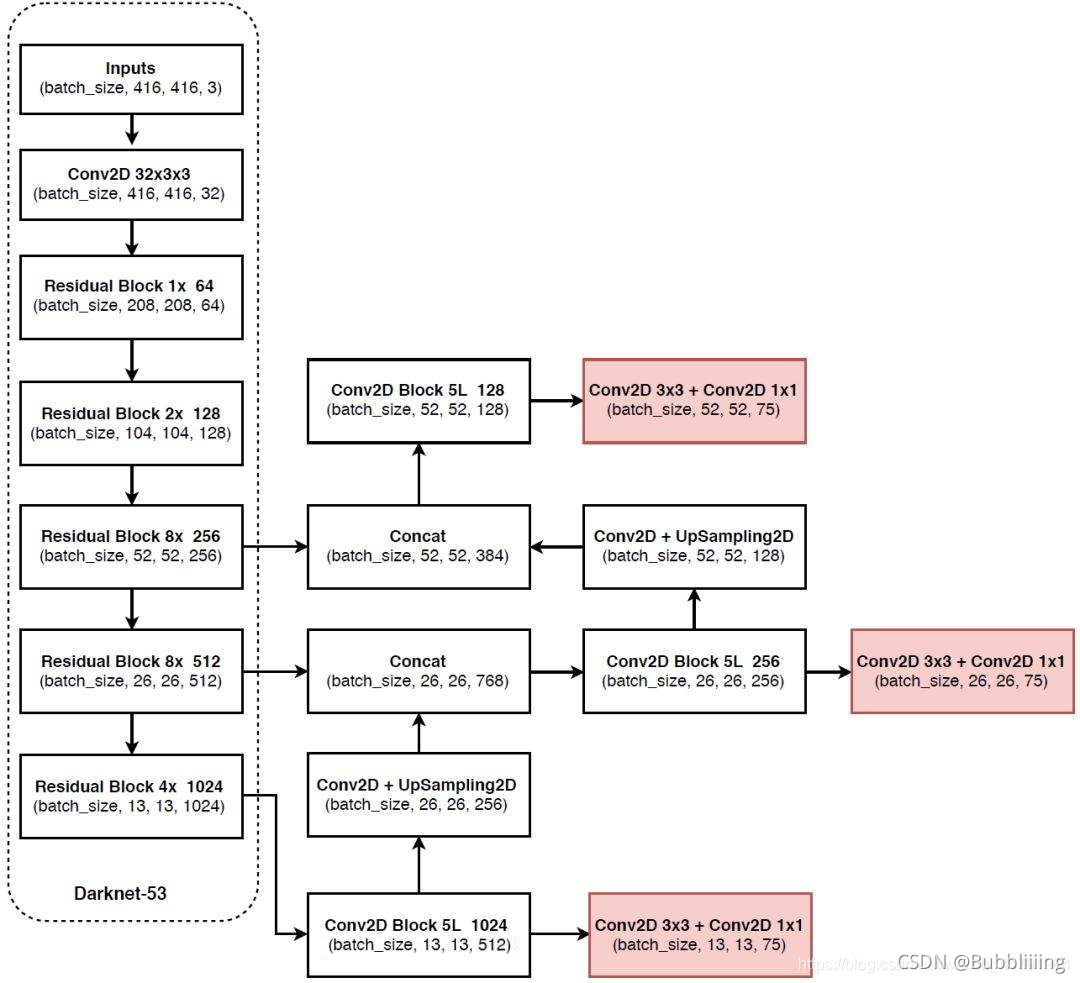
YOLOV3输出的75通道怎么来的?(对于VOC数据集来说,20class)
网上给出的答案是(5+20)x 3其中5代表(x,y,w,h,p),20是class,3是每个中心点3种box(还是anchor?)
我自己是这样理解:
5x3代表三种box的(w,y,h,w,p)
20x3代表20个类别属于三种box分别的概率
YoloV4
使用了SPP结构
类似FPN的PAnet结构
Loss用了CIOU,CIOU将目标与anchor之间的距离,重叠率、尺度以及惩罚项都考虑进去(重叠面积、中心点距离、长宽比),使得目标框回归变得更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。而惩罚因子把预测框长宽比拟合目标框的长宽比考虑进去
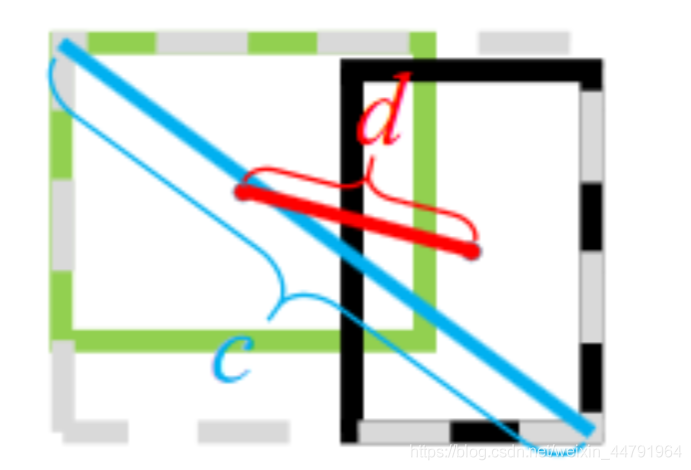
$$ CIOU = IOU - \frac{\rho^2(b,b^{gt})}{c^2}-\alpha \nu $$
其中$\rho^2(b,b^{gt})$分别代表了预测框和真实框的中心点的欧式距离。 c代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。
$$ \alpha = \frac{\nu}{1-IOU+\nu} \\ \nu = \frac{4}{\pi^2}(\arctan\frac{w^{gt}}{h^{gt}}-\arctan\frac{w}{h})^2 $$