范数与正则化
首先说明下范数和正则化的作用:为了使矩阵稀疏,作为惩罚项限制w矩阵参数值过大
当w为复杂矩阵时,也代表了w关注了更多的特征,因此当出现过拟合的时候我们应该尽可能使得w矩阵变得稀疏
范数正则化一般是用来解决过拟合问题的,L1正则化可以用来进行特征选择,正则化可以解决过拟合问题
在优化模型的时候,我们不仅要保证训练误差最小,我们更希望我们的模型测试误差小,所以我们需要加上第二项,也就是对参数w的规则化函数Ω(w)去约束我们的模型尽量的简单。
$$ w^*=\mathop{\arg\min}_{w} = \sum_i L(y_i,f(x_i;w)) + \lambda \Omega(w) $$
L-P范数不是一个范数,而是一组范数,定义如下:
$$ L_p= \sideset{^p}{\sqrt{\sum^n_ix^p_i}} \ , x=(x_1,x_2,...,x_n) $$
当p = 0 和 1时:
1. L0范数
L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。
$$ L_0= \sideset{^0}{\sqrt{\sum^n_ix^0_i}} \ , x=(x_1,x_2,...,x_n) $$
因为实际上0不能开方,所以L0难以用数学式表示,故被人认为是一个NP难问题。所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。
2.L1范数
L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)
L1范数也有一定的正则化能力,但是没有L2范数强
稀疏的原因是他在Wi=0的地方不可微
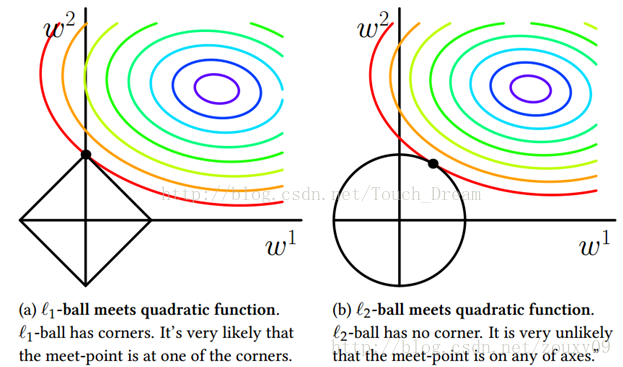
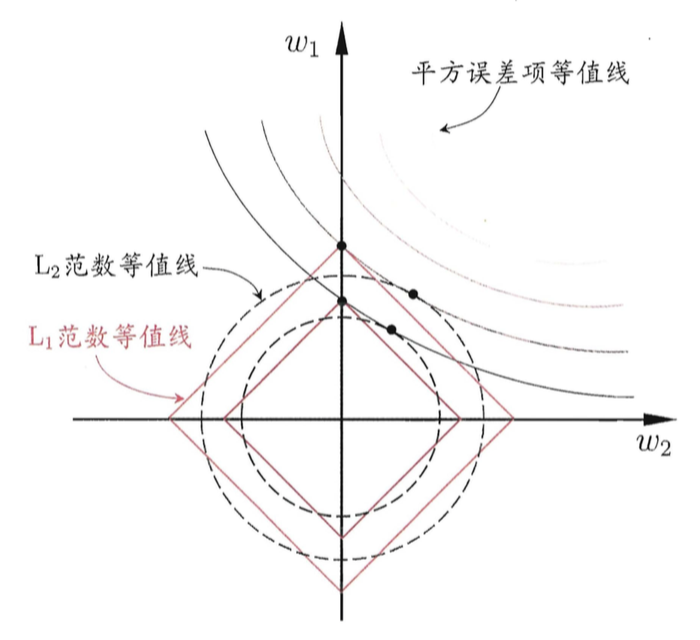
由图可见L1范数在w1=0处有角度,因此此处是不可导的
L1范式正则化更容易获得稀疏解
如图的L1范式中w2有值,w1取0,比起L2范式更稀疏
3.L2范数
L2范数是指向量各元素的平方和然后求平方根。L2正则化可以防止模型过拟合(overfitting)
4.联系与区别
总结:
- L1范式更容易获得稀疏解,L2的正则化能力更强。
- L1范式下降更快,L2的是坡度下降。
对于线性回归模型,使用L1正则化的模型建模叫做Lasso回归
对于线性回归,使用L2正则化的模型叫做Ridge回归(岭回归)
L1和L2都是规则化的方式,我们将权值参数以L1或者L2的方式放到代价函数里面去。
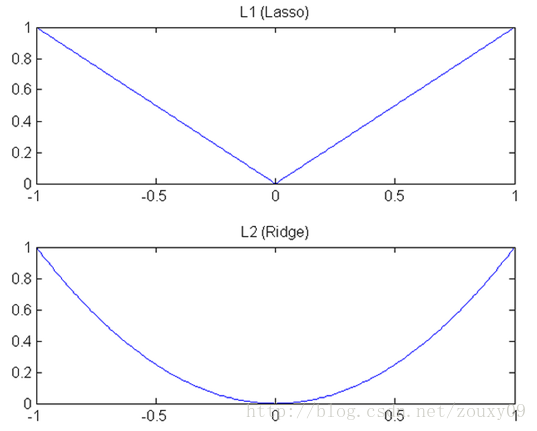
然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程,L1和L2的差别就在于这个“坡”不同,如下图:
L1就是按绝对值函数的“坡”下降的,而L2是按二次函数的“坡”下降。
所以实际上在0附近,L1的下降速度比L2的下降速度要快。所以会非常快得降到0。
5.稀疏的作用
1.特征的选择
稀疏规则化算子能自动选择更重要的特征,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
2.可解释性
参数越少,说明需要判断的特征就越少,w就越好解释
3.鲁棒性
可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;
但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』(鲁棒性强)。
ref:
https://blog.csdn.net/zouxy09/article/details/24971995
https://blog.csdn.net/weixin_36411839/article/details/81944812