CV相关
仿射变换
仿射变换主要是对图像的缩放,旋转,翻转和平移等操作的组合。
# 2.1 创建变换矩阵
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[100,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
# 2.2 完成仿射变换
dst = cv.warpAffine(img,M,(cols,rows))腐蚀
https://zhuanlan.zhihu.com/p/164619939
腐蚀的作用消除物体边界点,使目标缩小,可以消除小于结构元素的噪声点。cv.erode(img,kernel,iterations)
- img: 要处理的图像
- kernel: 核结构
- iterations: 腐蚀的次数,默认是1
开运算
开运算是先腐蚀后膨胀,可以消除亮度较高的细小区域
其作用是:分离物体,消除小区域。特点:消除噪点,去除小的干扰块,而不影响原来的图像。
闭运算
闭运算与开运算相反,先膨胀后腐蚀。可以消除细小黑色空洞,也不会明显改变其他物体区域面积。
作用是消除/“闭合”物体里面的孔洞,特点:可以填充闭合区域。
礼帽运算
原图像与“开运算“的结果图之差
因为开运算带来的结果是放大了裂缝或者局部低亮度的区域,因此,从原图中减去开运算后的图,得到的效果图突出了比原图轮廓周围的区域更明亮的区域,且这一操作和选择的核的大小相关。
礼帽运算用来分离比邻近点亮一些的斑块。当一幅图像具有大幅的背景的时候,而微小物品比较有规律的情况下,可以使用顶帽运算进行背景提取。
黑帽运算
为”闭运算“的结果图与原图像之差。
黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域,且这一操作和选择的核的大小相关。
黑帽运算用来分离比邻近点暗一些的斑块。
cv2.imshow()和plt.imshow()的区别
什么时候使用
plt.show(),什么时候用cv2.imshow()?
如果需要展示读入的图像,或者展示对读入图像进行一系列操作后的图像时,使用cv2.imshow()
如果不需要展示原始图像,而是绘制一张新的图像,使用plt.imshow()
其实两者都可以,但要注意的是opencv是BGR通道,plt默认RGB通道,若使用cv2.imread()读入图像,用plt.imshow()展示原始图像或者展示对读入图像进行一系列操作后的图像时,需要进行通道转换。
在展示灰度图像时,cv2.imshow(‘gray’, gray)plt.imshow(gray,cmap=‘gray’), plt.title(‘gray’)
滤波
均值滤波
将平均滤波器与原图进行卷积,由一个归一化卷积框完成的。它只是用卷积框覆盖区域所有像素的平均值来代替中心元素。
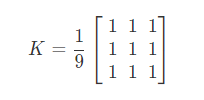
均值滤波的优点是算法简单,计算速度较快,缺点是在去噪的同时去除了很多细节部分,将图像变得模糊。
cv.blur(src, ksize, anchor, borderType)
- src:输入图像
- ksize:卷积核的大小
- anchor:默认值 (-1,-1) ,表示核中心
- borderType:边界类型
高斯滤波
在x,y上利用高斯分布的密度函数构造滤波器
正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
计算平滑结果时,只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
高斯平滑在从图像中去除高斯噪声方面非常有效。
具体方法是构建权重矩阵,然后用权重矩阵对原图进行卷积
cv2.GaussianBlur(src,ksize,sigmaX,sigmay,borderType)
src: 输入图像
ksize:高斯卷积核的大小,注意 : 卷积核的宽度和高度都应为奇数,且可以不同
sigmaX: 水平方向的标准差
sigmaY: 垂直方向的标准差,默认值为0,表示与sigmaX相同
borderType:填充边界类型
中值滤波
中值滤波是一种典型的非线性滤波技术,基本思想是用像素点邻域灰度值的中值来代替该像素点的灰度值。
中值滤波对椒盐噪声(salt-and-pepper noise)来说尤其有用,因为它不依赖于邻域内那些与典型值差别很大的值。缺点是,效率不如均值滤波;
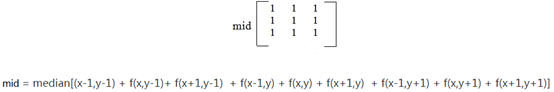
cv.medianBlur(src, ksize )边缘检测
Sobel算子
利用一阶导数求得像素产生变化的边界,抗噪声能力很强,用途较多。尤其是效率要求较高,而对细纹理不太关心的时候
对水平方向卷积
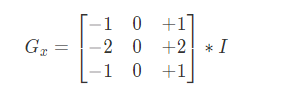
对垂直方向卷积
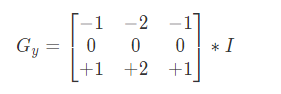
最后结合两个结果求出
$$ G=\sqrt{G_x^2+G_y^2} $$
sobel实现45°:
$$ [[-2,-1,0], \\ [-1,0,1], \\ [0,1,2]] $$
Laplacian算子(拉普拉斯算子)
利用二阶导数来检测边缘
Canny边缘检测
分为4步:
- 因为Canny容易被噪点影响,所以先进行高斯滤波器的降噪
- 对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数(Gx 和 Gy)。根据得到的这两幅梯度图(Gx 和 Gy)找到边界的梯度和方向
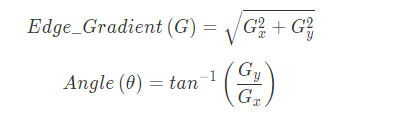
- 在每个$\theta$方向上,对边进行极大值抑制:去除非边上的点,检查所检测的像素点的周围像素,判断该检测点是否形成局部最大值
滞后阈值:
现在要确定真正的边界。 我们设置两个阈值: minVal 和 maxVal。 当图像的灰度梯度高于 maxVal 时被认为是真的边界, 低于 minVal 的边界会被抛弃。如果介于两者之间的话,就要看这个点是否与某个被确定为真正的边界点相连,如果是就认为它也是边界点,如果不是就抛弃。
霍夫变换
首先霍夫变换输入的应该是二值化图片
霍夫线变换
原理是将笛卡尔坐标系(也就是平时的xy坐标系)映射到霍夫空间中,并在霍夫空间中换成极坐标形态
$$ \rho = x\cos\theta+y\sin\theta $$
在霍夫空间中以$\theta$做x轴,$\rho$做y轴,有特性:在笛卡尔坐标系中,一条线上面的点就是霍夫空间上的一个点,反而来也成立,在霍夫空间上的一条线对应笛卡尔坐标系上的一个点
实现方法:
利用一个2D数组的累加器,本质上就是一个模拟的霍夫空间$\theta$做x轴,$\rho$做y轴;在上面将笛卡尔坐标系中的点在上面映射成模拟的直线,模拟的位置都+1.然后遍历笛卡尔坐标系上所有的感兴趣点,最后看累加器中,哪个位置的数最大,该点对应位置就是原图卡尔迪坐标上的线
Harris和shi-Tomas具有旋转不变性 但是不具有尺度不变性
Harris角点检测
原理是利用一个点的以及它周围的灰度值差异的总和来衡量该点是否是角
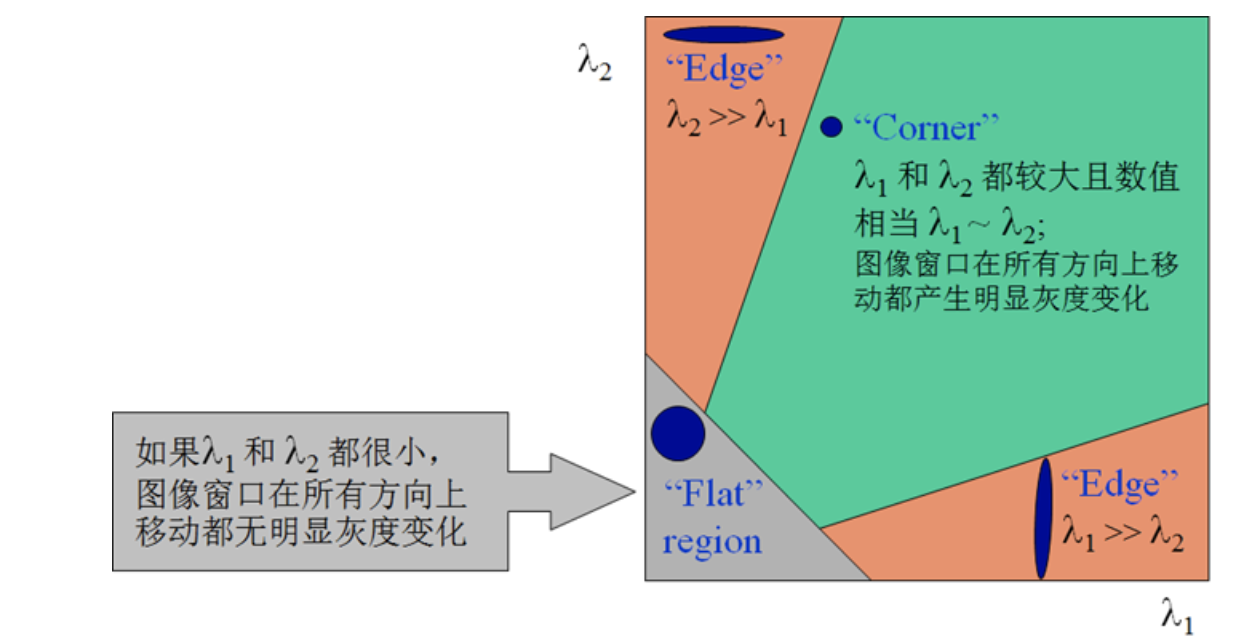
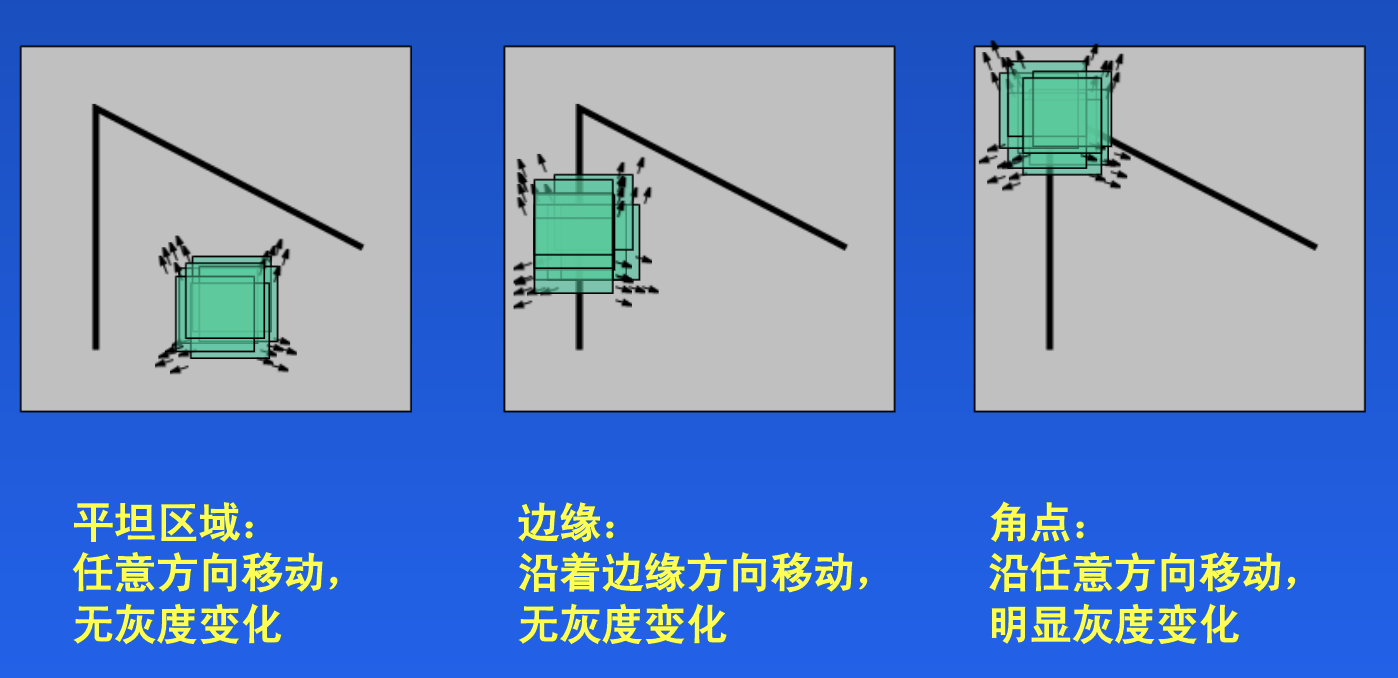 将它求灰度值均值的公式泰勒展开后,其中有个M矩阵决定了灰度值均值的值,这个矩阵的特征向量$\lambda_1
将它求灰度值均值的公式泰勒展开后,其中有个M矩阵决定了灰度值均值的值,这个矩阵的特征向量$\lambda_1
$和$\lambda_2$有如下关系:
SIFT
用来寻找图像之中的特征,能够用来匹配的
Harris算法可以根据它提取出的角只具有旋转不变性,但是不具有尺度不变性
而SIFT算法能够提取出 特征点 和 特征点描述 ,这些结果具有旋转不变性 和 尺度不变性,适合用来做匹配
主要分为两个大步骤:特征点检出 和 特征描述
特征点检出:
目标是提取出图像中符合旋转不变性 和 尺度不变性特征的点的位置,还有该点的产生变化的方向
提取位置:
为了检测出图像中变化度高的点,利用图像的二阶导数(即Log高斯拉普拉斯方法)来产生关键信息,为了减少计算量,使用两个高斯尺度空间的图像相减,来获得高斯差分(Dog)来近似Log
为了得到多尺度下的高斯差分(Dog),于是对图片做高斯金字塔进行下采样,并且在每次采样中获得的octave中,都利用不同比例的方差$\sigma$(如$k\sigma,k^2\sigma...$)的高斯核函数来高斯模糊该采样尺度下的图片,这里会产生多层同尺度的图片;
为了多尺度测量,,这里隔行、隔列取原图的像素点,然后将基础$\sigma$变为$2\sigma$(下一组基础$\sigma$变为$4\sigma$),在此基础上再如上面进行多次 不同比例的方差的高斯模糊 ,产生另一组octave,这组的octave尺度是原来图片的四分之一
就这样产生多组octave
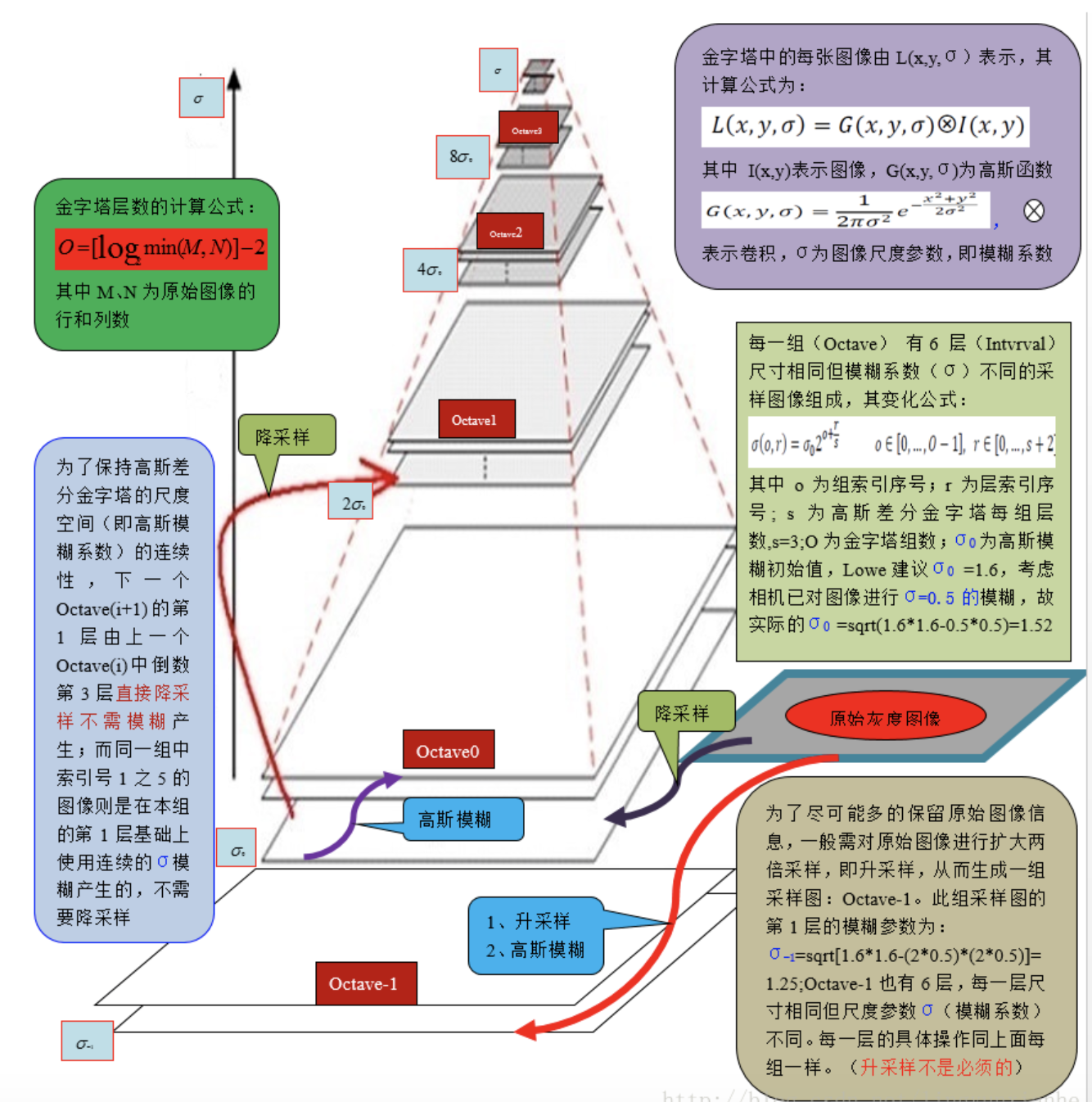
利用每组octave中的图片两两互减,得到高斯差分(Dog),
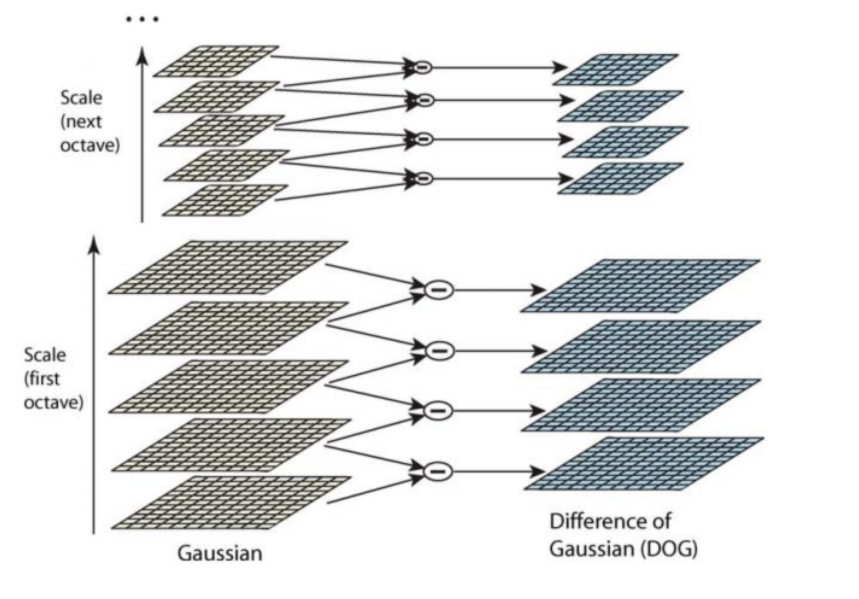
在 DoG 搞定之后,就可以在不同的尺度空间中搜索局部最大值了。对于图像中的一个像素点而言,它需要与自己周围的 8 邻域,以及尺度空间中上下两层中的相邻的 18(2x9)个点相比。如果是局部最大值,它就可能是一个关键点。基本上来说关键点是图像在相应尺度空间中的最好代表。如下图所示:
这样就得到感兴趣的点的坐标和金字塔层数了
由于Dog对噪声和边界敏感,在得到高斯差分金字塔中检测到的局部极值点后,在此基础上使用 Harris 算法排除边界上的兴趣点,并且排除对比度过低的点,最终得到我们感兴趣的点的最终坐标
提取方向
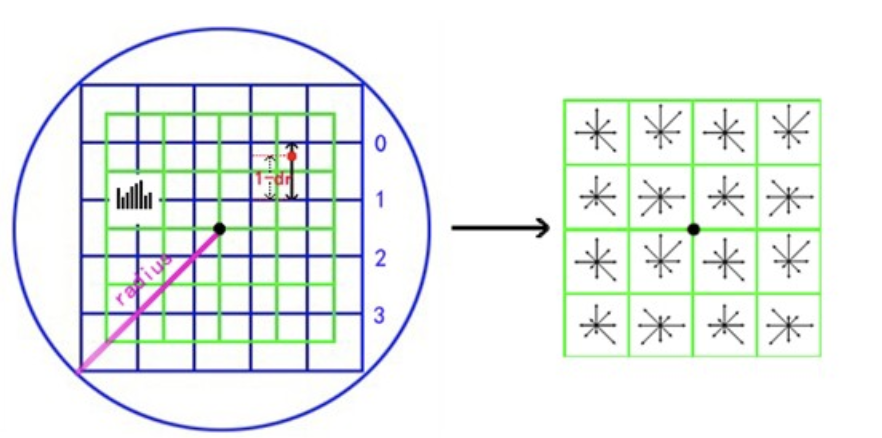
根据octave的图像金字塔每层的$\sigma$,在各特征点上划定不同半径的圆,计算圆内像素点的梯度方向和幅值,有点类似canny: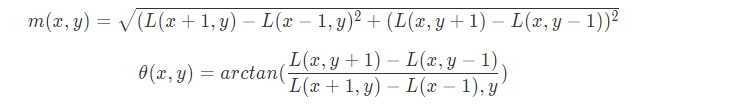
计算完梯度和幅值后,利用直方图计算这些圆中点八个方向的的幅度累加值(越靠近圆心幅度越高)
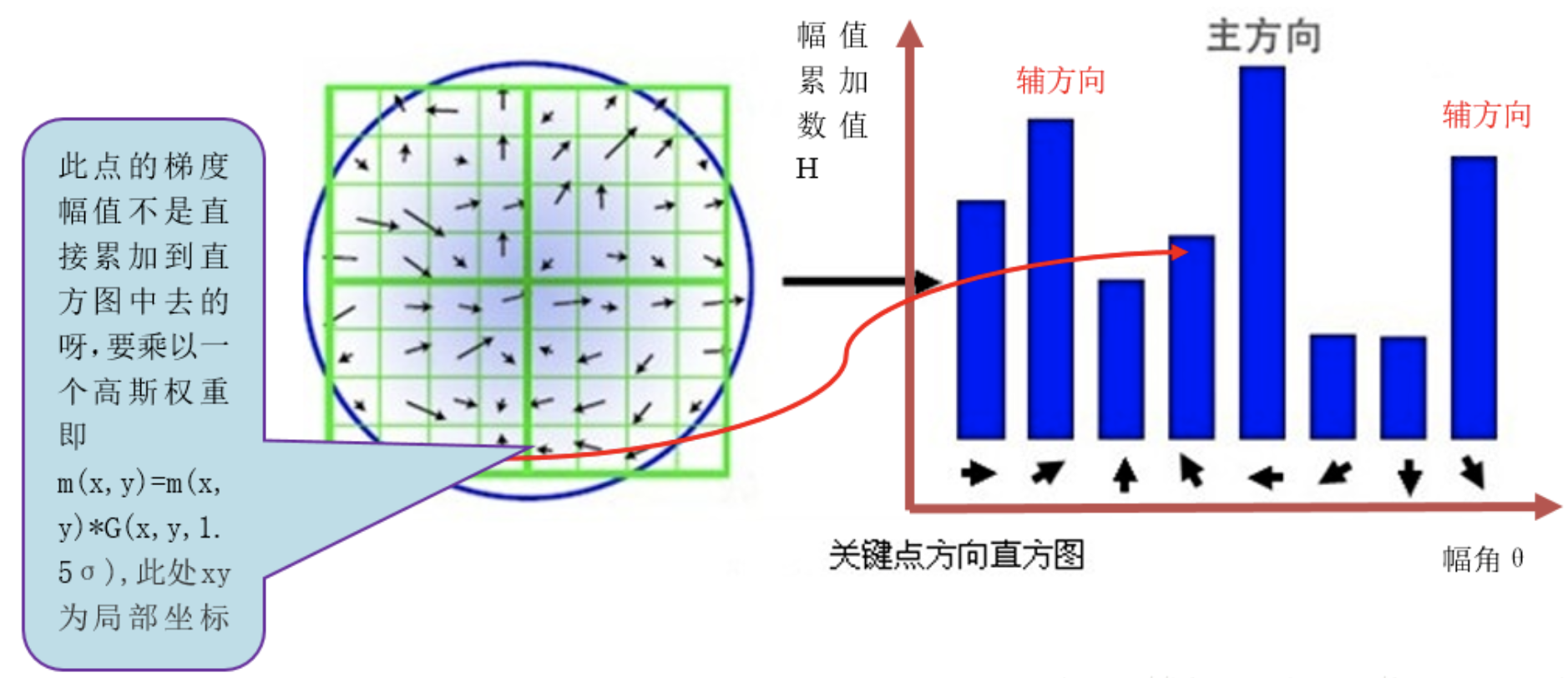
利用幅值大小确定该点的方向,
至此,利用金字塔图的特征尺寸不变性,将点映射会原图位置,我们就得到了关键点,也就是Sift特征点
每个关键点有三个信息(x,y,σ,θ):位置、尺度、方向
关键点描述
该结果是为了描述关键点周围的情况而做的
将每个关键点划分为dxd个子区域(d一般为4),每个区域边长为$3\sigma$(也就是子区域大小和尺度有关)
ps 区域的值最终用双线性插值确定
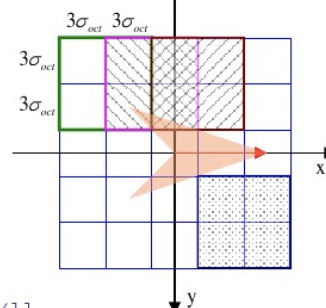
计算子区域的8个方向的像素梯度,并且用σ=0.5d进行高斯加权(越靠近中间权重越高)
最终,每个SIft特征点能获得$4*4*8=1284∗4∗8=128$个梯度信息作为该关键点的特征向量,也就是该点的特征描述。
机器学习
1.性能度量
$$ pre=\frac{TP}{TP+FP} \\ rec=\frac{TP}{TP+FN} \\ \frac{1}{F1}=\frac{1}{pre}+\frac{1}{rec} $$
ROC曲线:x轴假正例率,y轴真正例率,分别对应召回率和召假率
通过改变算法的阈值,画出算法的ROC曲线
通过比较两个算法ROC曲线的面积可判断哪个算法性能更好
AUC曲线,基于实际的例子,按点画出的曲线,不会有ROC那么平滑,实际上一般是计算AUC的面积
2.线性模型
https://www.cnblogs.com/muzixi/p/6642203.html
$$ f(x)=wx+b \\ (w^*,b^*)=\begin{array} aargmin \\ (w,b) \end{array} \ \sum^m_{i=1}(f(x_i)-y_i)^2 $$
求解方法:1.最小二乘法 2.梯度下降法
基于均方差进行模型求解的方法称为“最小二乘法”
在线性回归中,最小二乘法就是找到一条直线使所有样本到直线上的欧氏距离之和最小。
具体在另一篇文章中的线性最小二乘中的代数法和矩阵法
梯度下降法指的就是bp反向传播:
https://www.cnblogs.com/shona/p/10938533.html
3.感知模型
感知机(线性模型加了判断):
$$ f(x)=sign(wx+b)\\ sign(x) \begin{cases} +1 \ , \ x\ge0 \\ -1 \ , \ x<0 \end{cases} $$
学习方法:误分类点到分类超平面的总距离
(误分类说明预测的分类 (wx+b)和实际分类不一致,因此乘积为-1,而距离是绝对值,所以应该是 -y(wx+b)))
$$ L(w^*,b^*)=\begin{array} aargmin \\ (w,b) \end{array} \ -\sum^m_{i=1}y_if(x_i) $$
即当损失函数L(w,b)最小时的参数(w1,w2, ... , wn,b),便是最终模型中的参数。
可使用梯度下降来求解
ps 和SVM的区别:
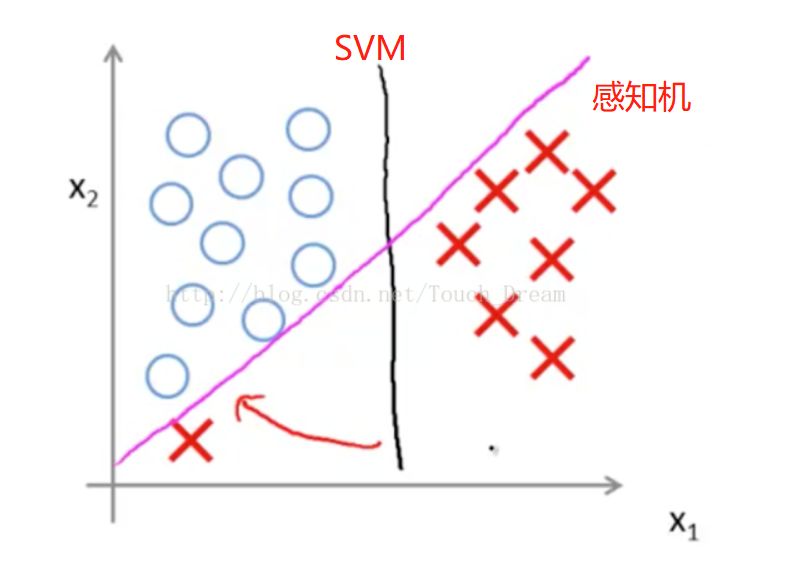
如上图所示,感知机的目标是尽可能使得所有样本分类正确,而SVM的目标是分类间隔最大化。
支持向量机追求大致正确分类的同时,一定程度上避免过拟合,效果类似上图中的黑线。
感知机使用的学习策略是梯度下降法,而SVM采用的是由约束条件构造拉格朗日函数,然后求偏导令其为0求得极值点。这里特别说明下一般我们的拉格朗日函数是符合凸函数的,因此对于凸函数一定存在极值点,也是唯一的最优解。而一般的非凸函数,只好采用梯度下降法一步一步的求得极值点,如果非凸函数还是采用求导令为0,可能找不到极值点!因为鞍点也是导数为0,但却不是极值点的特例,如$y = x^3$函数。导数为0是函数极值点的必要条件。
4.逻辑回归
$$ h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta x}} $$
本质是将线性回归的输出作为sigmoid函数的输入,最终的输出便是分类的结果。
模型解释:对于给定的x,输出y=1的概率
训练目标:根据训练数据学习参数
学习策略:条件概率p(y|x),表示x是输入,y是正确的输出的概率。学习策略即为求所有训练样本的条件概率之积的最大值。即要求概率之积尽可能大,这样模型的预测效果就会越准确。
损失函数:对数似然损失函数
$$ J(\theta)=\sum^m_{i=1}[y_i log h_\theta(x_i)+(1-y_i)log(1-h_\theta(x_i))] $$
可使用梯度下降来求解
5.SVM
略
线性核:$k(x_i,x_j)=x^T_ix_j$ 特征少,样本多
多项式核 :$k(x_i,x_j)=(x^T_ix_j)^d$ 其中d为可扩展的维度
高斯核:$k(x_i,x_j)=exp(-\frac{||x_i-x_j||^2}{2\sigma^2})$,$\sigma>0$为高斯核宽带
此外,和函数还可以线性组合如$\gamma_1k_1+\gamma_2k_2$
6.决策树
https://blog.csdn.net/gunhunti4524/article/details/81506012
ID3:
使用信息增益作为选择特征的准则;
ID3 仅仅适用于二分类问题。ID3 仅仅能够处理离散属性。
信息熵定义:
熵用于表示随机变量不确定性的度量
$$ Ent(D)=-\sum^{|y|}_{k=1}p_klog_2p_k $$
其中$p_k$为样本集合D中,第k类样本所占比例(用瓜的判断就分好瓜和坏瓜,此时y=2)
信息增益熵则为
$$ Gain(D,a)=Ent(D)-\sum^V_{v=1}\frac{|D^v|}{|D|}Ent(D^v) $$
其中a为离散属性有V个可能的取值${a^1,a^2,...,a^V}$(用瓜的判断就是{颜色、根蒂、纹理等}的属性)
(例如a=颜色时,v_1=绿色,v_2=黄色)
每次选择信息增益熵最大的为判断分支的依据
C4.5:
C4.5 使用信息增益比作为选择特征的准则;
$$ Gain\_ratio(D,a)=\frac{Gain(D,a)}{H(a)} \\ H(a)=-\sum^V_{v=1}\frac{|D^v|}{|D|}\log_2\frac{|D^v|}{|D|} $$
其中$H(a)$称为a的固有值,属性a能取的值越多,$H(a)$就越大
信息增益 vs 信息增益比
之所以引入了信息增益比,是由于信息增益的一个缺点。那就是:信息增益总是偏向于选择取值较多的属性。信息增益比在此基础上增加了一个罚项,解决了这个问题。
CART
CART 使用 Gini 指数作为选择特征的准则。
CART 的全称是分类与回归树(classification and regression tree)。从这个名字中就应该知道,CART 既可以用于分类问题,也可以用于回归问题。
不同于信息熵,CART使用Gini值来度量数据的纯度:
$$ Gini(D)=\sum^{|y|}_{k=1}\sum_{k`\neq1}p_kp_{k`}=1-\sum^{|y|}_{k=1}p^2_k $$
属性a的基尼指数定义为
$$ Gini\_index(D,a)=\sum^V_{v=1}\frac{|D^v|}{|D|}Gini(D^v) $$
不同于上面,基尼指数选择最小的为最优化分类
Gini 指数 vs 熵
既然这两个都可以表示数据的不确定性,不纯度。那么这两个有什么区别那?
Gini 指数的计算不需要对数运算,更加高效;
Gini 指数更偏向于连续属性,熵更偏向于离散属性。
剪枝
预剪枝:
一般使用留出法,在分支前进行判断
在当前节点,将其当作叶节点,类别为当前节点样本最多的类别数(好瓜最多就判断该节点为好瓜),然后用验证集算出当前节点准确率
确定最优属性a后,在划分的节点中再一起计算其准确率,与未分类之前的准确率作比较,若是准确率上升,则允许这个a属性的分支,否则不分。
优点是能够大幅度减少过拟合的风险,但是会带来欠拟合的风险
后剪枝:
当决策树生成完毕后,从叶节点开始向上再进行的剪枝
从叶子的父节点开始,将这个父节点当作叶节,计算验证集的准确率,若是准确率比分类后要高,那么进行剪枝
后剪枝的欠拟合风险很小,而且泛化性能往往要高于预剪枝,但是其训练的开销较大
7.贝叶斯
基于贝叶斯定理,求后验概率$P(c|x)$最大情况下,样本x 属于 类别c 的概率
例如c={c1:好瓜,c2:坏瓜},那么就比较$P(c_1|x)$和$P(c_2|x)$的概率,哪个大,x就属于那类
在生成式模型中,利用贝叶斯定理,将$P(c|x)$展开:
$$ P(c|x)=\frac{P(x,c)}{P(x)}=\frac{P(x|c)P(c)}{P(x)} $$
将上面问题变为求 条件概率$P(x|c)$ 和 先验概率 $P(c)$的问题
先验概率P(c)易求得
$$ P(c)=\frac{|D_c|}{|D|} $$
D为数据集
以下只介绍生成式模型的方法
极大似然估计
在极大似然估计中,我们认为假设的$P(x|c)$具有确定的,并且唯一的参数$\theta_C$,因此我们可以将$P(x|c)$表示为$P(x|\theta_c)$
假设这些样本之间是独立分布的,那么$P(D_c|\theta_c)$的似然有:
$$ P(D_c|\theta_c)=\prod_{x\in D_c}P(x|\theta_c) $$
为了不让连乘使得数据下溢,一般使用对数似然:
$$ LL(\theta_c)=\log \,P(D_c|\theta_c) \\ = \sum_{x\in D_c} \, \log P(x|\theta_c) $$
此时参数$\theta_c$最大似然解为
$$ \hat \theta_c =\ \underset {\theta_c}{arg \, max}LL(\theta_c) $$
算出$\hat \theta_c$后,用新的条件概率构建似然函数$P(x|c)$,再带入x算出概率
假设$P(x|c)$符合正态分布,那么极大似然估计$\theta_c={\mu_c,\sigma^2_c}$,即可做出似然函数的分布,相当于利用不同的c各自构造一个概率模型
朴素贝叶斯
所有属性之间要相互独立
我们将贝叶斯定理的
$$ P(c|x)=\frac{P(x|c)P(c)}{P(x)}=\frac{P(c)}{P(x)}\prod^d_{i=1} P(x_i|c) $$
d为属性数目,$x_i$为x在第i个属性上的取值
将上面提取出来,即本来比较$P(c|x)$变为比较:$P(c)\prod^d_{i=1} P(x_i|c)$,用公式表示,即
$$ h_{nb}(x) = \underset {c\in y} {arg \, max} P(c)\prod^d_{i=1} P(x_i|c) $$
那么条件概率$P(x_i|c)$可估计为
$$ P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|} $$
若是连续的概率密度函数$P(x_i|c)$,例如高斯分布$\mu_{c,i}$,$\sigma^2_{c,i}$,代表第c类样本在第i个属性上的取值和方差,直接带入$x_i,$$\mu_{c,i}$,$\sigma^2_{c,i}$利用高斯分布的概率密度函数直接算出概率即可
深度学习
语义分割
deeplab
v1系列,在vgg-16的基础上将倒数第三层的fc改成了使用空洞卷积代替的方法,并且将最后一层fc成做成CRF的全连接层,关于CRF:能够利用像素之间的位置和大小判断像素直接的关系,能够优化网络的输出结果
V2中,在V1的基础上,加上了aspp结果,替换了倒数第二层的上采样Fc,关于aspp:通过改变核的stride和卷积核的rate率(卷积都是3x3,但是通过空洞填充变成的边长)
V3中,规范化了网络结果,并且将basebone换成了Resnet50,利用串联卷积结构和Aspp。最后的输出:
- 一个3×3卷积做的是concat操作(过渡作用)
- 一个1×1卷积,改变输出通道数为num_class。
- 再将num_class张特征图使用bilinear的方式插值到输入图片的尺寸(相当于直接上采样了8倍),至此,得到了deeplabv3的输出。
完全抛弃了Fc层
V3+中,主干换成了Xception网络,在上面的基础上改变有:
- xception中带的depthwiseconv
- 重新设计了解码部分
解码部分利用了一部分地特征维度的信息,再结合最后Aspp输出后的信息最后经过3x3卷积后再上采样
FCN
主要贡献是提出了反卷积结构 和 结构跳跃,实现了全卷积结构
主干部分是Vgg-16
U-Net
UNet网络可以简单看为先下采样,经过不同程度的卷积,学习了深层次的特征,再经过上采样回复为原图大小,上采样用反卷积实现。
使用maxpool下采样,反卷积进行上采样,前面的特征concat到后面的特征再进行3x3的卷积
分类网络
EfficientNet
以一定的卷积层数、卷积层通道数、输入图片分辨率比例,在增加同等的Flops下来构建网络的大小,能取得最好的效果,比起同量级的分类卷积网络,拥有更小、更快、更准确的优势
w(卷积通道数的实现)直接把basebone中的卷积输出通道乘以w
d(卷积层数的实现)把basebone中例如resnet中的block数量乘以d
MobileNet
- 提出了反残差网络结构
- 使用SE提高了网络的注意力机制
- 提出了$h−swish[x]$ 函数代替了$swish[x]$ 函数,加快了sigmoid函数的运算速度
- 改进ASPP提出Lite R-Aspp
(logloss是二分类交叉熵)
Focal Loss解决样本分布不均匀的问题
Lovász-Softmax 作者使用了一种方法将iOu中的离散变量量化了,变成了线性插值函数,使得可以统计每个像素的损失
Iouloss":
$$ \frac{|T\bigcap P|}{|T|+|P|-|T\bigcap P|} $$
不建议在中间层使用Sigmoid激活函数,因为它会让梯度消失。
padding填充方法:
零填充ZeroPad2d、常数填充ConstantPad2d、镜像填充ReflectionPad2d、重复填充ReplicationPad2d
后续补充ing