1.欧氏距离
判断空间向量的相似程度:
$$ d=\sqrt{\sum^N_{i=1}(x_{1i}-x_{2i})^2} $$
2.余弦距离
其实就是计算空间向量的夹角值
$$ d=1-similarly \\ similarly=cos(\theta)=\frac{A . B}{||A|| \ ||B||}=\frac{\sum^n_{i=1}A_iB_i}{\sqrt{\sum^n_{i=1}A^2_i}\sqrt{\sum^n_{i=1}B^2_i}} $$
使用场景
欧氏距离体现数值上的绝对差异
余弦距离体现方向上的相对差异
1)例如,统计两部剧的用户观看行为,用户A的观看向量为(0,1),用户B为(1,0);此时二者的余弦距很大,而欧氏距离很小;
我们分析两个用户对于不同视频的偏好,更关注相对差异,显然应当使用余弦距离。
2)而当我们分析用户活跃度,以登陆次数(单位:次)和平均观看时长(单:分钟)作为特征时,余弦距离会认为(1,10)、(10,100)两个用户距离很近;
但显然这两个用户活跃度是有着极大差异的,此时我们更关注数值绝对差异,应当使用欧氏距离。
可以利用数值增加来判断数据应该注重数值还是方向
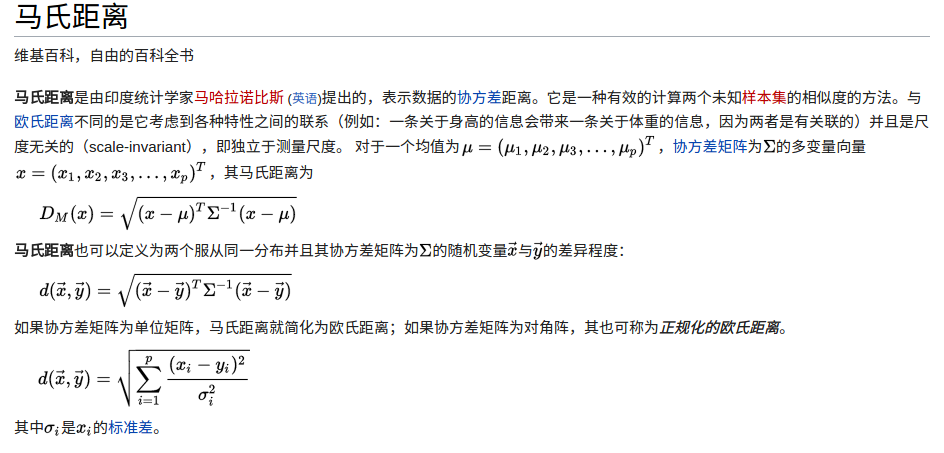
4.马氏距离
https://blog.csdn.net/bluesliuf/article/details/88862918
https://zhuanlan.zhihu.com/p/80660109
表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是*它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。
马氏距离可以利用一组数据的分布去预测另一组数据分布的拟合程度
现在有一组数据$Y=(Y_1,Y_2...Y_n)$,Y展开为m维 其均值为$u=(u_1,u_2,...,u_n)$
Y展开后行为样本数,列为变量数,即一个$Y_i$代表一组变量
利用公式$\sum = \frac{1}{m-1}(Y-u)^T(Y-u)$求得协方差矩阵,大小为$n*n$
(这里可见如果样本数越多,所求的协方差矩阵求得的协方差会越准确)
现在有另一组多变量向量X$X=(X_1,X_2,...,X_n)$,假设该为变量的均值$\mu=(\mu_1,\mu_2,...,\mu_n)$的的马氏距离为:
其中$X_i$展开为列向量,一个$X$完全展开后,行数代表样本,列数代表变量数
$$ D_M(X)=\sqrt{(X-\mu)^T(\sum)^{-1}(X-\mu)} $$
我们可以发现如果$(\sum)^{-1}$是单位阵的时候,马氏距离简化为欧氏距离。
那我们为什么要用马氏距离呢?
马氏距离有很多优点: 马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。
马氏距离除以了一个方差矩阵,这就把各个分量之间的方差都除掉了,消除了量纲性,更加科学合理。
计算机中马氏距离的实现
观察公式可知$D_M(X)=\sqrt{(X-\mu)^T(\sum)^{-1}(X-\mu)}$中的协方差矩阵是逆的,但是现实中有可能协方差矩阵并不是可逆的,也就是它是一个半正定矩阵,为了求解马氏距离,我们需要使用一些方法代替矩阵求逆
马氏距离实际上是利用 Cholesky transformation 来消除不同维度之间的相关性和尺度不同的性质。假设样本点(列向量)之间的协方差对称矩阵是 $\sum$ ,通过 Cholesky Decomposition(实际上是对称矩阵 LU 分解的一种特殊形式)可以转化为下三角矩阵和上三角矩阵的乘积:$\sum=LL^T$ 。消除不同维度之间的相关性和尺度不同,只需要对样本点 x 做如下处理: $Z=L^{-1}(x-\mu)$ 。处理之后的欧几里得距离就是原样本的马氏距离:
为了书写方便,这里求马氏距离的平方):
$D_M(X)=\$
$= Z^TZ$
$= (L^{-1}(x-\mu))^T(L^{-1}(x-\mu))$
$= (x-\mu)^T(LL)^T(x-\mu)$
$= (x-\mu)^T(\sum)^{-1}(x-\mu)$
在程序中使用np.linalg.cholesky求协方差的下三角矩阵$L$
再使用scipy.linalg.solve_triangular求解$L^{-1}(x-\mu)$
def gating_distance(self, mean, covariance, measurements,
only_position=False):
# 计算状态分布和测量值之间的门控距离
#mean为均值 covariance为协方差矩阵 measurements为要预测的向量组
"""Compute gating distance between state distribution and measurements.
A suitable distance threshold can be obtained from `chi2inv95`. If
`only_position` is False, the chi-square distribution has 4 degrees of
freedom, otherwise 2.
Parameters
----------
mean : ndarray
Mean vector over the state distribution (8 dimensional).
covariance : ndarray
Covariance of the state distribution (8x8 dimensional).
measurements : ndarray
An Nx4 dimensional matrix of N measurements, each in
format (x, y, a, h) where (x, y) is the bounding box center
position, a the aspect ratio, and h the height.
Returns
-------
ndarray
Returns an array of length N, where the i-th element contains the
squared Mahalanobis distance between (mean, covariance) and
`measurements[i]`.
"""
# Cholesky分解,得到covariance分解的的正定lower triangle矩阵cholesky_factor
# 有covariance = np.dot( cholesky_factor , cholesky_factor.T )
cholesky_factor = np.linalg.cholesky(covariance)
d = measurements - mean
z = scipy.linalg.solve_triangular(
cholesky_factor, d.T, lower=True, check_finite=False,
overwrite_b=True)
# 以下等价于np.dot(z,z.T)
squared_maha = np.sum(z * z, axis=0)
return squared_maha # 马氏距离